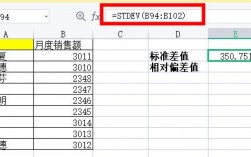
如何计算标准差

标准差定义与重要性

标准差（Standard Deviation）是统计学中用于描述数据分散程度的一个重要指标，它表示数据集中每个数值与数据集的算术平均值之间的平均偏差，并经过平方和取平均后的平方根运算得出，标准差能反映一个数据集的离散程度，即数据值与其平均值的差异大小，在正态分布中，标准差尤为重要，因为它能够揭示数据分布的特性。

标准差的类型

根据计算方式的不同，标准差可分为两种主要类型：总体标准差（Population Standard Deviation）和样本标准差（Sample Standard Deviation）。

总体标准差

总体标准差用于描述整个总体数据的离散程度，其计算公式为：

\[ \sigma = \sqrt{\frac{\sum_{i=1}^{N} (x_i \mu)^2}{N}} \]

\(\sigma\) 表示总体标准差；

\(N\) 表示总体中数据的数量；

\(x_i\) 表示每一个数据点；

\(\mu\) 表示总体数据的均值。

样本标准差

样本标准差用于描述从总体中抽取的样本数据的离散程度，其计算公式为：

\[ s = \sqrt{\frac{\sum_{i=1}^{n} (x_i \bar{x})^2}{n1}} \]

\(s\) 表示样本标准差；

\(n\) 表示样本中数据的数量；

\(x_i\) 表示每一个样本数据点；

\(\bar{x}\) 表示样本数据的均值。

注意：样本标准差分母使用 \(n1\) 而不是 \(n\)，这是因为样本标准差要估计总体标准差，使用 \(n1\) 可以得到无偏估计。

计算步骤详解

计算均值

无论是总体标准差还是样本标准差，首先需要计算数据集的均值，对于给定数据集 \(x_1, x_2, ..., x_n\)，均值的计算公式为：

\[ \bar{x} = \frac{\sum_{i=1}^{n} x_i}{n} \]

示例：

假设有一个数据集 [95, 85, 75, 65, 55]，首先计算其均值：

\[ \bar{x} = \frac{95 + 85 + 75 + 65 + 55}{5} = \frac{375}{5} = 75 \]

计算每个数据点与均值的差的平方

计算每个数据点与均值的差的平方：

\[ (x_i \bar{x})^2 \]

示例继续：

\[

\begin{align*}

(95 75)^2 &= 400 \\

(85 75)^2 &= 100 \\

(75 75)^2 &= 0 \\

(65 75)^2 &= 100 \\

(55 75)^2 &= 400 \\

\end{align*}

\]

求和并计算方差

将所有平方差求和：

\[ \sum_{i=1}^{n} (x_i \bar{x})^2 \]

然后除以 \(n\) 或 \(n1\) 得到方差：

\[ \text{方差} = \frac{\sum_{i=1}^{n} (x_i \bar{x})^2}{n} \quad \text{或} \quad \frac{\sum_{i=1}^{n} (x_i \bar{x})^2}{n1} \]

示例继续：

\[

\sum_{i=1}^{5} (x_i 75)^2 = 400 + 100 + 0 + 100 + 400 = 1000

\]

如果是总体标准差：

\[ \text{方差} = \frac{1000}{5} = 200 \]

如果是样本标准差：

\[ \text{方差} = \frac{1000}{4} = 250 \]

求方差的平方根得到标准差

将方差的平方根计算出，即为标准差：

\[ \sigma = \sqrt{\text{方差}} \]

或

\[ s = \sqrt{\text{方差}} \]

示例继续：

对于总体标准差：

\[ \sigma = \sqrt{200} \approx 14.14 \]

对于样本标准差：

\[ s = \sqrt{250} \approx 15.81 \]

标准差是统计学中衡量数据离散程度的关键指标，通过上述步骤可以准确计算总体标准差和样本标准差，理解并正确应用标准差有助于分析数据波动情况，评估数据的可靠性以及进行进一步的统计分析。