二进制计算是计算机科学和数字电子技术中的基础概念,它使用0和1两个数字进行运算,二进制系统在现代电子设备中广泛应用,因为它与电子设备的开关状态(开/关)直接对应,使得硬件设计和数据处理更加高效。
一、二进制数的基本概念
二进制是一种基数为2的数字系统,每一位称为一个比特(bit),代表0或1两种状态,每个比特的位置从右到左依次为2的0次方、2的1次方、2的2次方等,二进制数1011可以表示为:
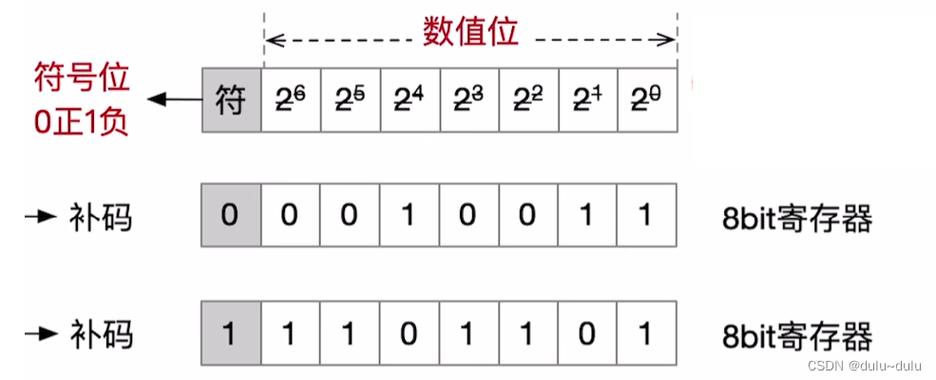
\[ 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 = 8 + 0 + 2 + 1 = 11 \]
二、二进制数的算术运算
1. 加法
二进制加法遵循“逢二进一”的规则,具体法则如下:
0 + 0 = 0
0 + 1 = 1 + 0 = 1
1 + 1 = 0(进位为1)

1 + 1 + 1 = 1(进位为1)
示例:计算1110和1011相加的过程如下:
1110 + 1011 11001
2. 减法
二进制减法遵循“借一有二”的规则,具体法则如下:
0 0 = 0
1 1 = 0
1 0 = 1
0 1 = 1(借位为1)
示例:计算1101减去1011的过程如下:
1101 1011 0010
3. 乘法
二进制乘法过程类似于十进制乘法,但由于只有0和1两种可能的乘数位,因此更为简单,法则如下:
0 × 0 = 0
0 × 1 = 1 × 0 = 0
1 × 1 = 1
示例:计算1001和1010相乘的过程如下:
1001
× 1010
0000 (1010的最低位是0,所以部分积是0)
+ 1001 (左移一位,因为1010的次低位是1)
+ 1001 (左移两位,因为1010的第三位是1)
= 100110014. 除法
二进制除法与十进制除法类似,通过重复减去除数得到商数和余数,法则如下:
如果被除数大于或等于除数,则商为1,否则商为0。
将被除数减去除数后,将余数与下一位组合继续比较。
示例:计算100110÷110的过程如下:
110 | 100110
| 110
|
0110
110
000三、二进制数的逻辑运算
1. 逻辑“或”运算(OR)
规则如下:
0 OR 0 = 0
0 OR 1 = 1 OR 0 = 1
1 OR 1 = 1
示例:计算X=00FFH和Y=5555H的逻辑“或”运算:
00FFH OR 5555H 55FFH
2. 逻辑“与”运算(AND)
规则如下:
0 AND 1 = 0 OR 1 AND 0 = 0
1 AND 0 = 0 OR 1 AND 1 = 1
1 AND 1 = 1
示例:计算X=00FFH和Y=5555H的逻辑“与”运算:
00FFH AND 5555H 0055H
3. 逻辑“非”运算(NOT)
规则如下:
NOT 0 = 1
NOT 1 = 0
示例:计算X=00FFH的逻辑“非”运算:
NOT 00FFH = FF00H
4. 逻辑“异或”运算(XOR)
规则如下:
0 XOR 0 = 0
0 XOR 1 = 1 XOR 0 = 1
1 XOR 0 = 1 XOR 1 = 1
1 XOR 1 = 0
示例:计算X=00FFH和Y=5555H的逻辑“异或”运算:
00FFH XOR 5555H 55AAH
四、二进制数的转换
1. 二进制转十进制
将每位的值乘以对应的2的幂次然后求和,二进制数1011转换为十进制:
\[ 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 = 8 + 0 + 2 + 1 = 11 \]
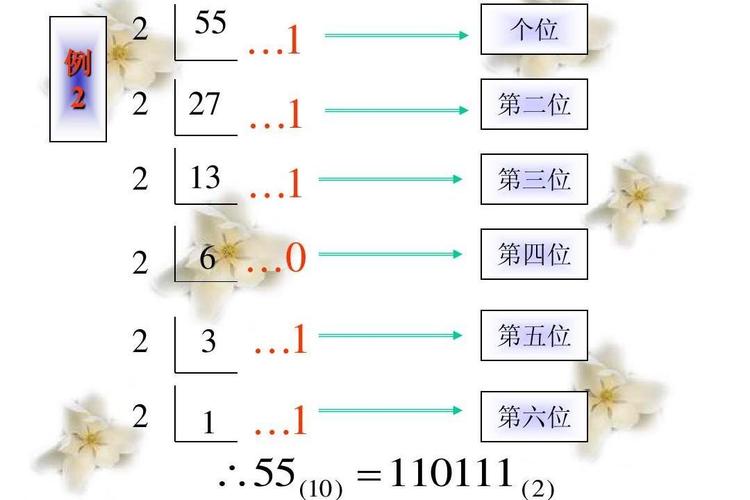
2. 十进制转二进制
不断除以2并记录余数,最后将余数反转,十进制数21转换为二进制:
\[ 21 / 2 = 10 ... 1 \]
\[ 10 / 2 = 5 ... 0 \]
\[ 5 / 2 = 2 ... 1 \]
\[ 2 / 2 = 1 ... 0 \]
\[ 1 / 2 = 0 ... 1 \]
反转余数得到二进制数:10101。
五、实际应用中的二进制计算
1. 计算机内部数据表示和处理
计算机中的所有数据,包括文本、图片、音频和视频,最终都以二进制形式存储,硬盘、SSD等存储设备中的信息也以比特为单位进行存储。
2. 网络通信中的编码和解码
在网络通信中,数据在传输过程中以二进制形式进行编码和解码,不同的协议确保了信息的完整性和有效性。
3. 编程语言中的底层实现
大多数编程语言底层都是基于二进制运算的,程序员编写的高级代码最终会被编译器转换为二进制机器码,以便计算机执行。
4. 网络安全中的加密算法
加密算法通常使用二进制数进行运算,以确保数据的安全性和隐私性,二进制的特性使其非常适合用于复杂的加密算法。
六、相关FAQs
Q: 为什么计算机使用二进制而不是十进制?
A: 因为计算机是基于电子电路工作的,而电子电路只有两种状态:开和关,正好对应二进制的0和1,这使得二进制在硬件设计和数据处理上更加高效。
Q: 如何将二进制数转换为十六进制数?
A: 每四位二进制数转换为一位十六进制数,二进制数1101转换为十六进制是D,具体步骤是将二进制数从右到左每四位一组,不足四位的在前面补零,然后将每组转换为相应的十六进制数字。