常见的平均数类型及计算方法
1、算术平均数:
定义:又称均值,是统计学中最基本、最常用的一种平均指标,它分为简单算术平均数和加权算术平均数。
简单算术平均数:适用于未分组的原始数据,设一组数据为 X1,X2,...,Xn,其计算公式为:\(\bar{x}=\frac{x_1 + x_2 + \cdots + x_n}{n}\)。
加权算术平均数:主要用于处理经分组整理的数据,设原始数据被分成 K 组,各组的组中值为 X1,X2,...,Xk,各组的频数分别为 f1,f2,...,fk,其计算公式为:\(\bar{x}=\frac{x_1f_1 + x_2f_2 + \cdots + x_kf_k}{f_1 + f_2 + \cdots + f_k}\)。
2、调和平均数:
定义:又称倒数平均数,是总体各统计变量倒数的算术平均数的倒数,分为简单调和平均数(数值倒数的平均数的倒数)和加权调和平均数(计算结果与加权算术平均数完全相等)。
简单调和平均数:设一组数据为 X1,X2,...,Xn,其计算公式为:\(\frac{n}{\frac{1}{x_1}+\frac{1}{x_2}+\cdots+\frac{1}{x_n}}\)。
加权调和平均数:设原始数据被分成 K 组,各组的组中值为 X1,X2,...,Xk,各组的频数分别为 f1,f2,...,fk,其计算公式为:\(\frac{f_1 + f_2 + \cdots + f_k}{\frac{f_1}{x_1}+\frac{f_2}{x_2}+\cdots+\frac{f_k}{x_k}}\)。
应用场合:可以用于计算平均速度,例如计算 4x100 米接力赛中运动员的总体速度。
3、几何平均数:
定义:对各变量值的连乘积开项数次方根,根据所掌握资料的形式不同,其分为简单几何平均数和加权几何平均数两种形式。
简单几何平均数:设一组数据为 X1,X2,...,Xn,其计算公式为:\(G=\sqrt[n]{x_1x_2\cdots x_n}\)。
加权几何平均数:设原始数据被分成 K 组,各组的组中值为 X1,X2,...,Xk,各组的频数分别为 f1,f2,...,fk,其计算公式为:\(G=\sum_{i = 1}^{k}f_i\sqrt{\prod_{j = 1}^{i}x_j}\div\sum_{i = 1}^{k}f_i\)。
应用场合:对比率、指数等进行平均;计算平均发展速度;复利下的平均年利率;连续作业的车间产品的平均合格率;计算总水平、总成果等所有阶段、所有环节水平、成果的连乘积总和时,求各阶段、各环节的一般水平、一般成果,要使用几何平均法计算几何平均数。
1、常规法:先求两个数之和,再除以二(右移一位),这种方法适用于简单的两个数的平均数计算,但可能会导致数据溢出问题。
2、差值法:将另外几个数依次和最小的数相减,再把它们的差全部加起来,最后除以个数,和最小的数相加,这种方法可以避免数据溢出问题,但计算过程相对复杂一些。
3、求同异法:通过求两个数比特位相同部分的差,以及不同的部分,来得到最终的平均数,这种方法利用了二进制的特性,对于计算机来说操作较为高效。
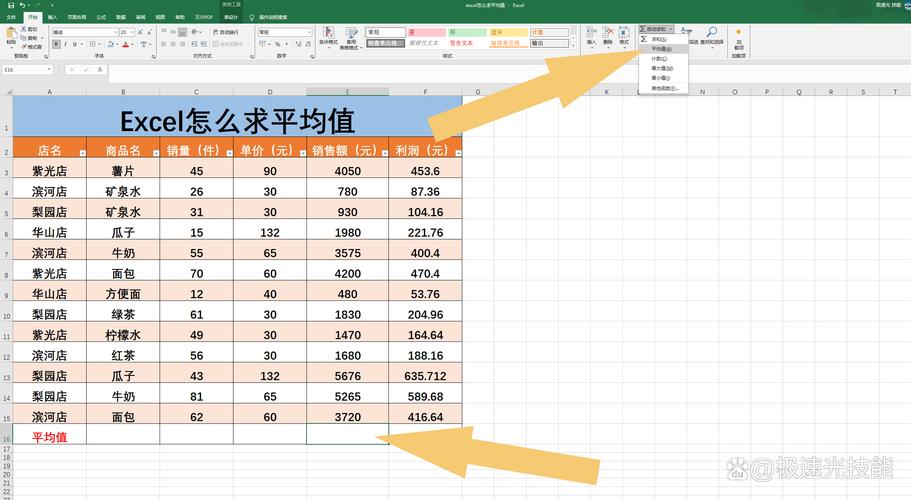
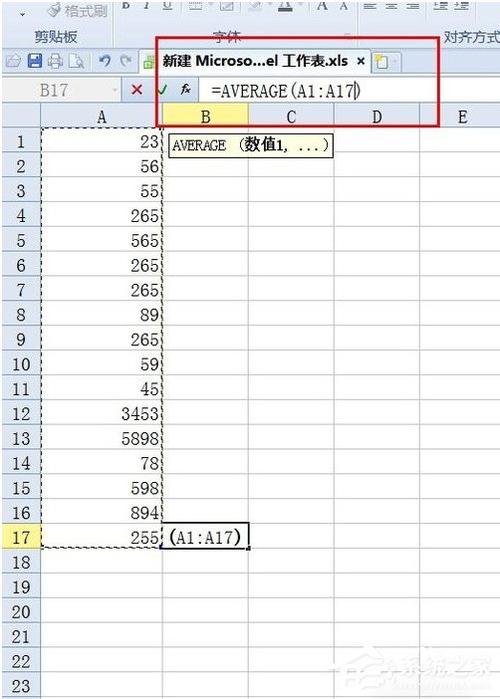
4、快捷键公式法:在 Excel 中,可以使用快捷键 Alt+M 键,然后选择“平均值”公式,快速求出表格中某一行或某一列的平均分。
FAQs
1、Q: 如何选择合适的平均数计算方法?
A: 选择合适的平均数计算方法取决于数据的特点和应用的需求,如果数据没有明显的极端值,且需要反映数据的集中趋势,算术平均数是一个常用的选择,如果数据存在极端值,或者需要强调数据的中间水平,可以考虑使用中位数或众数,如果需要计算平均速度、平均发展速度等,调和平均数或几何平均数可能更合适。
2、Q: 为什么算术平均数容易受极端值的影响?
A: 算术平均数是通过将所有数据相加后除以数据的数量来计算的,因此每个数据都会对结果产生影响,如果存在极端值(即非常大或非常小的值),它们会显著地影响总和,从而导致算术平均数偏离数据的集中趋势,相比之下,中位数和众数不受极端值的影响,因此在数据存在极端值时可能更能反映数据的中心位置。