递归报错解析与解决指南
递归是一种在编程中常用的技术,它允许函数或过程直接或间接地调用自身,递归算法简洁而强大,但同时也容易引发错误,特别是如果递归条件设置不当或递归深度过大时,本文将详细探讨递归报错的常见原因、解决方法以及如何优化递归算法以避免错误和提高效率。
一、递归报错的常见原因
| 错误类型 | 描述 | 示例 |
| 栈溢出错误 | 递归过深,导致调用栈溢出 | factorial(10000)(未优化) |
| 无限递归 | 递归没有正确的终止条件 | function loop() { loop(); } |
| 逻辑错误 | 递归逻辑不正确,导致结果错误 | 错误的斐波那契数列计算 |
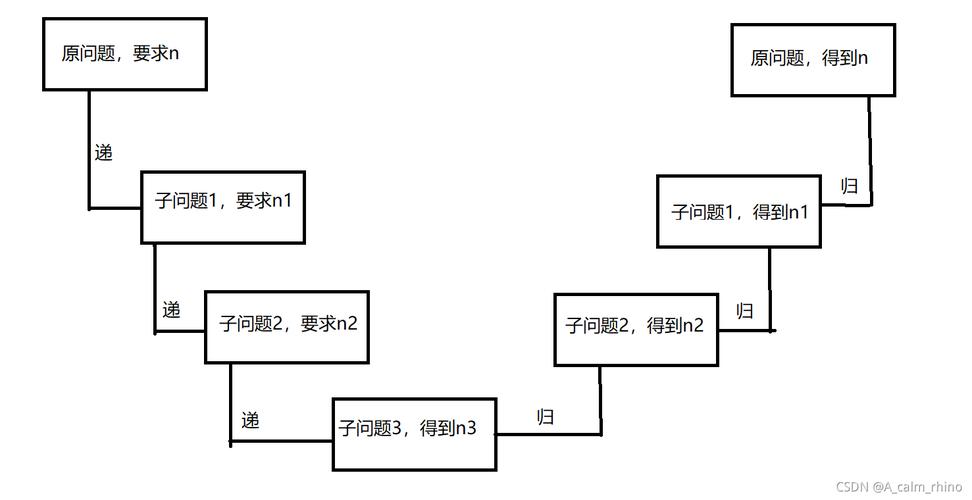
1. 栈溢出错误
递归算法中,每次函数调用都会在调用栈上增加一个帧,如果递归太深,调用栈可能会溢出,导致程序崩溃,计算大数的阶乘时,如果没有适当的优化,很容易造成栈溢出。
解决方案:
尾递归优化:如果递归的最后一步是自身调用,可以考虑使用尾递归优化。
迭代替代:将递归转换为迭代,避免深度递归。
限制递归深度:设定递归深度限制,防止无限递归。

2. 无限递归
无限递归发生在函数没有正确的终止条件时,导致函数无限调用自身。
解决方案:
检查终止条件:确保每个递归函数都有明确的终止条件。
调试与测试:通过调试和单元测试来验证递归逻辑的正确性。
3. 逻辑错误
即使递归能够正常结束,也可能存在逻辑错误,导致结果不正确。
解决方案:
仔细审查逻辑:确保递归逻辑符合问题描述。
使用测试用例:通过不同的测试用例来验证递归函数的正确性。
二、递归算法优化技巧
为了提高递归算法的性能和稳定性,可以采用以下优化技巧:
1. 记忆化递归(Memoization)
记忆化递归通过存储已经计算过的结果来避免重复计算,从而提高效率。
def fibonacci(n, memo={}):
if n in memo:
return memo[n]
if n <= 1:
return n
memo[n] = fibonacci(n1, memo) + fibonacci(n2, memo)
return memo[n]2. 动态规划(Dynamic Programming)
动态规划通过构建一个表格来保存中间结果,避免重复计算。
def fibonacci(n):
if n <= 1:
return n
dp = [0] * (n+1)
dp[1] = 1
for i in range(2, n+1):
dp[i] = dp[i1] + dp[i2]
return dp[n]3. 尾递归优化
尾递归是一种特殊的递归形式,其中递归调用是函数体中的最后一个操作,许多编程语言可以优化尾递归,减少调用栈的使用。
def tail_recursive_factorial(n, acc=1):
if n == 0:
return acc
return tail_recursive_factorial(n1, n*acc)三、案例分析
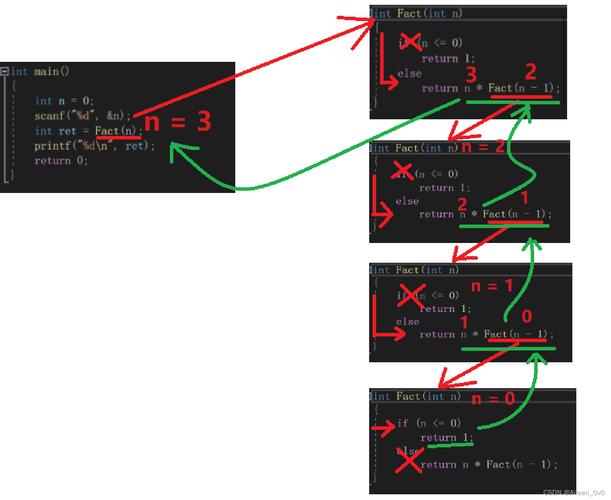
案例1:阶乘函数的优化
原始的阶乘函数可能导致栈溢出:
def factorial(n):
if n == 0:
return 1
return n * factorial(n1)优化后的阶乘函数使用尾递归:
def tail_recursive_factorial(n, acc=1):
if n == 0:
return acc
return tail_recursive_factorial(n1, n*acc)案例2:斐波那契数列的优化
原始的斐波那契数列计算效率低下:
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n1) + fibonacci(n2)使用记忆化递归优化:
def fibonacci(n, memo={}):
if n in memo:
return memo[n]
if n <= 1:
return n
memo[n] = fibonacci(n1, memo) + fibonacci(n2, memo)
return memo[n]四、归纳
递归是一种强大的编程技术,但也需要谨慎使用以避免错误和性能问题,通过理解递归报错的常见原因,并采用适当的优化技巧,我们可以编写出高效且稳定的递归算法,在实际开发中,建议结合迭代方法和递归方法,根据具体问题选择合适的解决方案。
FAQs
Q1: 什么是尾递归?
A1: 尾递归是一种特殊的递归形式,其中递归调用是函数体中的最后一个操作,这种形式的递归可以被某些编程语言优化,以减少调用栈的使用,从而提高性能。
Q2: 如何避免递归中的栈溢出错误?
A2: 避免栈溢出错误的方法包括:使用尾递归优化、将递归转换为迭代、设定递归深度限制以及使用记忆化递归或动态规划来减少不必要的计算。