fsolve报错详解

在使用fsolve函数解决复杂非线性方程时,可能会遇到各种报错,本文将详细解析这些错误的原因,并提供相应的解决方案,以下是对fsolve报错问题的全面分析:
一、常见报错及原因分析
1、数组大小不兼容
错误信息:对于此运算,数组的大小不兼容。
原因分析:这种错误通常是因为数组的维数或大小不匹配导致的,需要检查代码中的数组定义和运算是否正确。
解决方案:确保所有参与运算的数组具有相同的维度或使用适当的矩阵操作来调整它们的大小。
2、初始目标函数计算失败
错误信息:Failure in initial objective function evaluation. FSOLVE cannot continue.
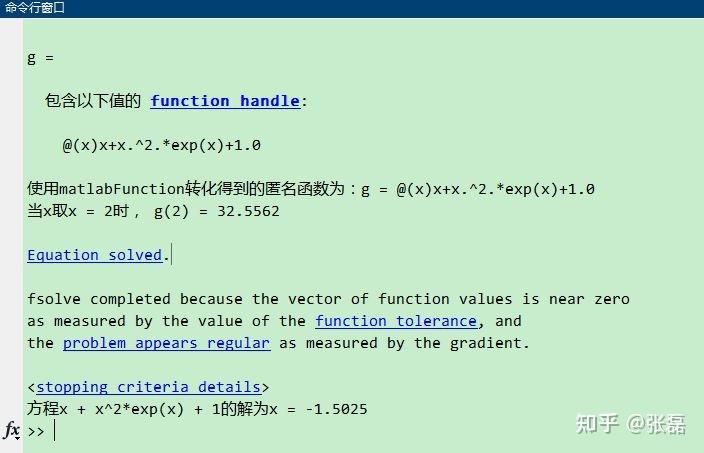
原因分析:这个错误通常是因为初始值不合理或者函数本身存在问题,需要检查代码中的函数表达式和初始值是否正确。
解决方案:手动调整初始猜测的值,确保它们足够接近解,检查函数是否符合fsolve函数的要求,并且没有语法错误。
3、算法无法处理非方阵系统
错误信息:Trustregiondogleg algorithm不能处理非方阵系统;使用LevenbergMarquardt算法代替。
原因分析:fsolve函数默认使用的trustregiondogleg算法无法处理非方阵系统。
解决方案:在fsolve函数中添加选项来指定算法类型,例如使用LevenbergMarquardt算法。
二、优化策略与建议
1、调整初始值
初始值对fsolve的影响很大,选择不合适的初始值可能导致无法求解,可以尝试更改初始值,看看是否能够求解。
2、检查方程是否有解
如果方程组没有解,fsolve函数会提示no solution found,重新检查方程组是否正确。
3、确保函数连续且光滑
fsolve函数要求函数是连续的且具有一定的光滑性,如果函数不具备这些条件,可能导致无法求解,检查函数是否满足这些条件。
4、更改算法参数
如果算法不收敛,可以尝试更改算法参数,如增加迭代次数或调整容差等。
5、使用其他数值求解方法
如果以上方法都不能解决问题,可以尝试使用其他数值求解方法,或者手动解方程组。
三、案例分析
以下是一个具体的案例,展示了如何使用fsolve函数解决非线性方程组,并处理可能出现的错误:
% 定义非线性方程组
function [y] = myfun(x)
y(1) = exp(exp((x(1)+x(2)))) x(2)*(1+x(1)^2);
y(2) = x(1)*cos(x(2)) + x(2)*sin(x(1)) 0.5;
end
% 初始猜测值
x0 = [0, 0];
% 调用fsolve函数求解
options = optimoptions('fsolve','Algorithm','levenbergmarquardt'); % 指定算法类型为LevenbergMarquardt
try
x = fsolve(@myfun, x0, options);
disp('Solution found:');
disp(x);
catch ME
disp('Error encountered:');
disp(ME.message);
end在这个例子中,我们首先定义了一个非线性方程组myfun,然后提供了一个初始猜测值x0,我们使用fsolve函数求解这个方程组,并指定了算法类型为LevenbergMarquardt,我们使用trycatch结构来捕获并处理可能出现的错误。
四、相关问答FAQs
Q1: fsolve函数提示“对于此运算,数组的大小不兼容”怎么办?
A1: 这个错误通常是因为数组的维数或大小不匹配导致的,需要检查代码中的数组定义和运算是否正确,确保所有参与运算的数组具有相同的维度或使用适当的矩阵操作来调整它们的大小。
Q2: fsolve函数提示“Failure in initial objective function evaluation. FSOLVE cannot continue.”怎么办?
A2: 这个错误通常是因为初始值不合理或者函数本身存在问题,需要检查代码中的函数表达式和初始值是否正确,手动调整初始猜测的值,确保它们足够接近解,检查函数是否符合fsolve函数的要求,并且没有语法错误。