浮点数报错解析
在计算机科学与编程领域,浮点数(floatingpoint number)因其能够表示实数范围内的值而得到广泛应用,由于其存储和计算方式的特性,浮点数运算有时会引发一系列问题,如精度缺失、溢出、除以零等错误,本文将详细探讨浮点数报错的常见原因、类型及其解决方案,并通过表格形式对比分析不同编程语言中浮点数的处理差异。
浮点数基础
浮点数是一种用于近似表示实数的数值类型,它在计算机中的存储遵循IEEE 754标准,该标准定义了浮点数的二进制表示形式,包括符号位、指数位和尾数位,常见的浮点数类型有单精度(32位,通常称为float)和双精度(64位,通常称为double)。
1.1 浮点数表示法
以64位的双精度浮点数为例,其结构如下:
符号位(S): 1位,0表示正数,1表示负数。
指数位(E): 11位,用以表示2的幂次,采用偏移量编码方式。
尾数位(M): 52位,表示有效数字。
这种结构使得浮点数能在一个相对较小的内存空间内表示很大范围的数值,但其本质是一种舍入近似。
1.2 浮点数精度问题
浮点数的精度问题源于其有限的位数,十进制下看似简单的小数0.1,在二进制中是一个无限循环小数,无法精确表示,只能通过近似值存储,这导致在进行数学运算时,尤其是涉及加减法和比较操作时,可能会出现意料之外的结果。
浮点数报错类型及案例分析
2.1 精度缺失
案例:在Python中,0.1 + 0.2的结果并非期望的0.3,而是0.30000000000000004。
解析:这是因为0.1和0.2在二进制中都是无限循环小数,相加后结果也是一个近似值,从而产生精度误差。
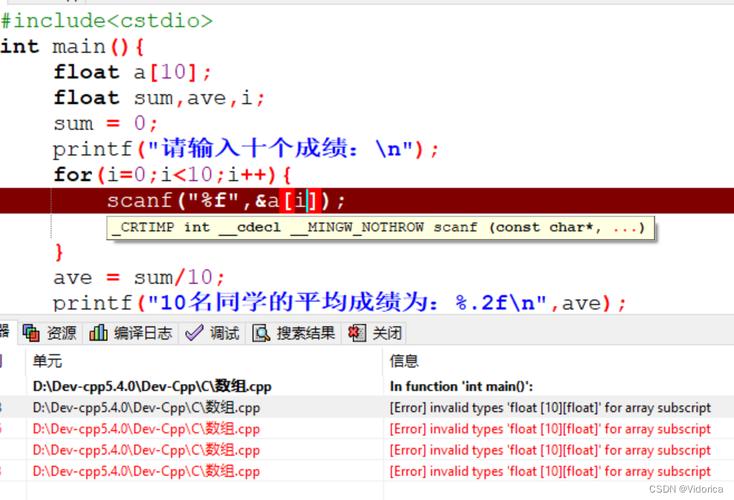
2.2 溢出错误
案例:在C++中,尝试将一个超出float范围的数值赋给一个float变量,如float a = 1e40;
解析:这将导致溢出,结果是未定义行为或特定实现下的最小正浮点数。
2.3 除以零
案例:在任何编程语言中,float b = 10 / 0;都会引发运行时错误或返回特殊值(如NaN Not a Number)。
解析:除以零是数学上未定义的操作,在编程中需避免或特别处理。
编程语言中的浮点数处理差异
下表展示了Python、Java、C++三种语言对同一浮点数运算的处理结果:
| 运算 | Python (float) | Java (float) | C++ (float) |
| 0.1 + 0.2 | 0.30000000000000004 | 0.3 | 0.300000012 |
| 1e40 / 1e38 | inf | Infinity | inf |
| 1 / 0 | nan | NaN | NaN |
从表中可以看出,尽管各语言都遵循IEEE 754标准,但由于内部实现细节和舍入策略的不同,具体结果会有细微差别。
解决浮点数问题的策略
1、使用更高精度的数据类型:当float不足以满足需求时,可考虑使用double甚至高精度库(如Python的decimal)。
2、避免直接比较:由于精度问题,应使用一个小的阈值来判断两个浮点数是否“足够接近”。
3、数值稳定算法:选择或设计算法时,优先考虑数值稳定性,减少运算过程中的误差累积。
4、异常处理:对于可能的除以零、溢出等情形,做好异常捕获和处理。
浮点数作为计算机科学中不可或缺的一部分,其报错问题反映了理论与实践之间的微妙平衡,理解浮点数的工作原理、认识其局限性并采取相应的预防措施,是进行科学计算和软件开发时的重要技能,随着技术的发展,虽然我们无法完全消除浮点数的所有问题,但通过合理的设计和编码习惯,可以最大限度地减少它们带来的影响。
FAQs
Q1: 为什么即使很小的浮点数加减运算也可能导致大的误差?
A1: 这是因为浮点数的表示是基于二进制系统的,许多十进制下看似简单的小数在二进制中变成了无限循环小数,只能通过有限位数近似表示,加减运算时,这些近似值参与计算,每一步都可能引入新的舍入误差,当这些误差累积起来,就可能导致最终结果与预期有较大偏差。
Q2: 如何判断两个浮点数是否相等?
A2: 直接使用等号(==)比较两个浮点数是否相等通常是不可靠的,因为微小的精度差异会导致比较失败,正确的做法是定义一个非常小的阈值(称为“机器精度”或“epsilon”),如果两个浮点数之差小于这个阈值,则认为它们是相等的,在Python中可以使用math.isclose()函数来实现这一比较。