P值(Pvalue)是统计学中的一个重要概念,用于假设检验中判断统计结果是否具有统计学意义,P值反映了在原假设为真的情况下,观察到的样本数据或更极端情况出现的概率,以下是关于P值如何计算的详细解释:
一、P值的基本概念
P值是指在原假设H0成立的条件下,观察到当前统计量或更极端值的概率,它用于衡量样本数据与原假设之间的差异程度,从而决定是否拒绝原假设。

二、P值的计算方法
P值的计算取决于所使用的统计检验方法,如t检验、z检验、卡方检验等,不同的检验方法对应不同的P值计算公式。
1、t检验和z检验:
对于左侧检验,P值为检验统计量小于样本统计值的概率,即P = P{ X < C}。
对于右侧检验,P值为检验统计量大于样本统计值的概率,即P = P{ X > C}。
对于双侧检验,P值为检验统计量落在样本统计值两侧尾部区域内的概率的两倍,即P = 2 * min(P{ X < C}, P{ X > C}),当C位于分布曲线的右端时,使用前半部分;当C位于分布曲线的左端时,使用后半部分。
2、卡方检验:

卡方检验的P值通常通过查找卡方分布表来确定,或者使用统计软件进行计算。
3、ANOVA方差分析:
ANOVA方差分析的P值也是通过统计软件计算得出,用于检验多组数据均值是否存在显著差异。
4、SPSS中的P值计算:
在使用SPSS进行假设检验时,SPSS会自动计算并显示P值,在独立样本t检验中,SPSS会计算两组样本均值的差异是否显著,并给出相应的P值。
三、P值的解释与应用
计算出P值后,需要将其与给定的显著性水平α进行比较,以作出检验的上文归纳:
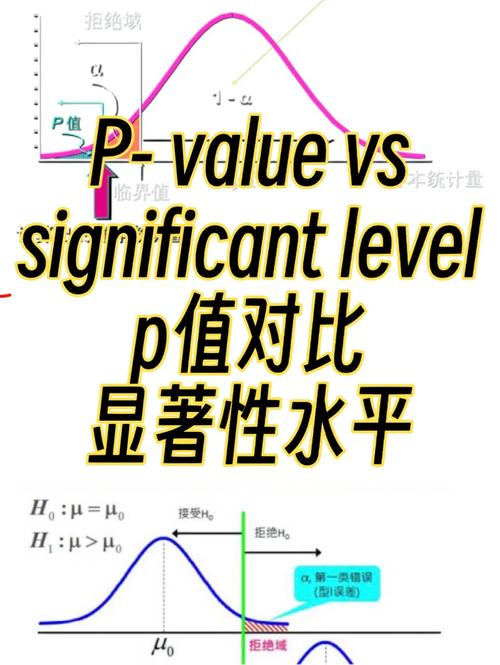
如果P > α,则在显著性水平α下接受原假设H0,认为样本间的差异不具有统计学意义。
如果P ≤ α,则在显著性水平α下拒绝原假设H0,认为样本间的差异具有统计学意义。
在实际应用中,通常选择α = 0.05作为显著性水平,这意味着如果P值小于0.05,则认为结果具有统计学意义。
四、注意事项
P值只是用来衡量数据的显著性,不能赋予数据任何重要性,它只能说明某事件发生的几率,而不能绝对地告诉原假设是对还是错。
当样本量很大时,即使很小的差异也可能导致P值很小,因此解释假设检验的结果时需要小心。
P值的计算是统计学假设检验中不可或缺的一部分,它帮助我们判断样本数据是否支持原假设,通过理解P值的概念、计算方法和应用场景,我们可以更好地利用统计工具来分析和解释数据,需要注意的是,P值只是统计推断中的一个工具,其结果需要结合实际情况和专业知识进行综合判断。
六、相关问答FAQs
问:什么是P值?
答:P值是在原假设为真的前提下,观察到当前样本数据或更极端情况出现的概率,它用于衡量样本数据与原假设之间的差异程度。
问:如何根据P值判断是否拒绝原假设?
答:将计算出的P值与给定的显著性水平α进行比较,如果P > α,则接受原假设;如果P ≤ α,则拒绝原假设,通常选择α = 0.05作为显著性水平。










