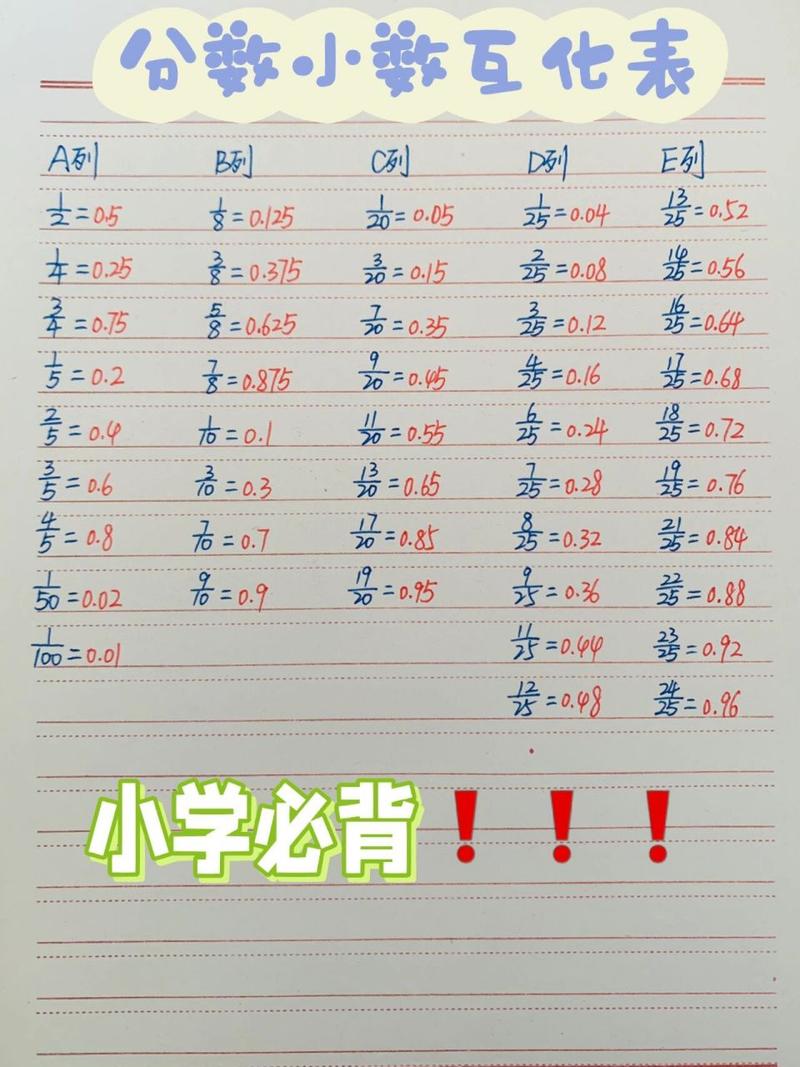
小数化分数是数学中一个常见且重要的操作，它涉及到有限小数和无限循环小数的转换，下面将详细介绍小数化分数的方法，并通过表格形式展示不同类型小数的转换过程：
1、确定小数的类型
（图片来源网络，侵权删除）
有限小数：小数点后有有限位数的小数，如0.75、0.125等。
无限循环小数：小数点后有固定的循环节，如0.333...、0.123123...等。
无限不循环小数：小数点后没有固定循环节，如π、e等。
2、有限小数转换为分数
步骤
将小数表示为分数。
（图片来源网络，侵权删除）
将分数进行约分，得到最简分数。
示例
将0.75转换为分数：
0.75 = 75/100 = 3/4将0.125转换为分数：
0.125 = 125/1000 = 1/83、无限循环小数转换为分数
步骤
（图片来源网络，侵权删除）
设x为该无限循环小数。
将x乘以适当的10的幂次，使循环节前移。
用得到的新等式减去原等式，消去循环部分。
解方程得到x的值，即该无限循环小数对应的分数。
示例
将0.333...转换为分数：
设 x = 0.333...
10x = 3.333...
10x x = 3.333... 0.333...
9x = 3
x = 1/3将0.123123...转换为分数：
设 x = 0.123123...
1000x = 123.123...
1000x x = 123.123... 0.123...
999x = 123
x = 123/999 = 41/3334、无限不循环小数（无理数）
无限不循环小数（如π、e等）不能精确地转换为分数，但可以通过逼近的方法用分数表示其近似值。π可以近似表示为22/7或更精确的分数形式。
表格展示
| 小数类型 | 转换方法描述 | 示例 | 结果 |
| 有限小数 | 将小数表示为分数，并进行约分 | 0.75 > 75/100 > 3/4 | 3/4 |
| 0.125 > 125/1000 > 1/8 | 1/8 | ||
| 无限循环小数 | 设x为该无限循环小数，通过方程求解 | 0.333... > x = 1/3 | 1/3 |
| 0.123123... > x = 41/333 | 41/333 | ||
| 无限不循环小数（无理数） | 使用逼近的方法表示其近似值 | π > 22/7 | 22/7 |
相关FAQs
1、为什么有限小数可以直接转换为分数？
答案：有限小数的小数部分有一个确定的结束点，因此可以直接将其表示为分子除以10的适当幂次的形式，然后进行约分以得到最简分数。
2、如何确定无限循环小数的循环节长度？
答案：无限循环小数的循环节是指小数部分中重复出现的那一部分数字序列，通过观察小数的重复模式，可以确定循环节的长度和具体数字序列，在转换过程中，这个长度决定了需要乘以的10的幂次数，以便消去循环部分并求解方程。
