约分是数学中简化分数的过程，其目标是将分数转换成最简形式，即分子和分母之间没有公因数，这一过程在数学运算中尤为重要，因为最简形式的分数更易于计算，也便于理解和比较，本文将详细介绍如何进行约分，包括步骤、示例、技巧以及常见问题解答。

一、约分的基本概念

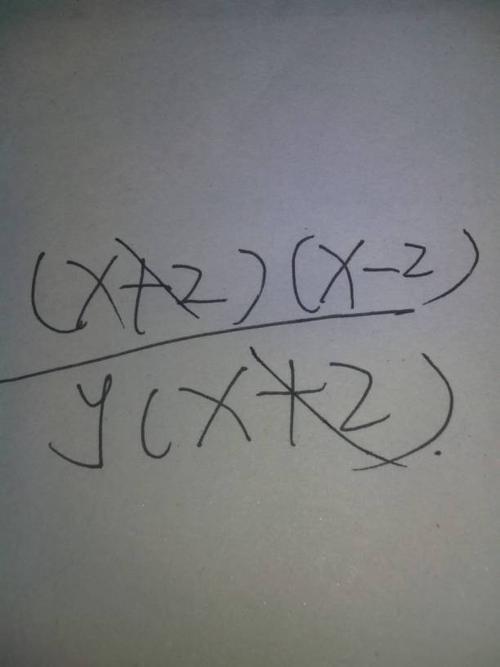
约分是指将一个分数化简到最简形式的过程，最简形式指的是分子和分母的最大公约数为1的分数形式，\(\frac{4}{8}\) 可以约分为 \(\frac{1}{2}\)，因为4和8的最大公约数是4。

二、约分的步骤

约分通常包括以下几个步骤：

1、找出分子和分母的最大公约数（GCD）：这一步可以通过列举因数、使用辗转相除法（欧几里得算法）等方法来实现。

2、用最大公约数去除分子和分母：将分子和分母同时除以它们的最大公约数。

3、简化分数：经过上述步骤后，得到的新分数即为最简形式。

三、约分的方法

1. 列举因数法

这种方法适用于较小的数字，通过列出分子和分母的所有因数，找到最大的公因数。

将 \(\frac{12}{18}\) 约分：

12的因数有：1, 2, 3, 4, 6, 12

18的因数有：1, 2, 3, 6, 9, 18

两者的最大公约数是6

\(\frac{12}{18} = \frac{12 \div 6}{18 \div 6} = \frac{2}{3}\)。

2. 辗转相除法（欧几里得算法）

对于较大的数字，辗转相除法更为高效，步骤如下：

用较大数除以较小数，得到余数。

然后用较小数除以余数，继续得到新的余数。

重复此过程，直到余数为0，最后一个非零余数就是最大公约数。

求14和21的最大公约数：

21 ÷ 14 = 1 余 7

14 ÷ 7 = 2 余 0

14和21的最大公约数是7。

3. 特殊技巧

如果分数的分子或分母含有平方因子，可以先提取平方根再约分，\(\frac{50}{36}\) 可以写成 \(\frac{50}{6^2}\)，进一步约分为 \(\frac{5 \times 5}{6 \times 6} = \frac{25}{36}\)。

四、约分的注意事项

不要改变分数的大小，只能通过除以共同的因数来简化。

确保最终的分子和分母互质，即最大公约数为1。

在进行复杂计算时，保持耐心，逐步检查每一步的正确性。

五、实例演示

让我们通过几个例子来加深理解：

例1：\(\frac{48}{60}\)

列举因数法：48的因数有1, 2, 3, 4, 6, 8, 12, 16, 24, 48；60的因数有1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60，最大公约数是12。

\(\frac{48}{60} = \frac{48 \div 12}{60 \div 12} = \frac{4}{5}\)。

例2：\(\frac{75}{50}\)

辗转相除法：50 ÷ 75 = 0 余 50；75 ÷ 50 = 1 余 25；50 ÷ 25 = 2 余 0，最大公约数是25。

\(\frac{75}{50} = \frac{75 \div 25}{50 \div 25} = \frac{3}{2}\)。

六、归纳与建议

约分是数学中一项基本而重要的技能，掌握它可以帮助更好地理解分数及其运算，以下是一些建议：

练习：多做练习题，熟悉各种约分方法。

工具使用：对于复杂的分数，可以使用计算器或在线工具辅助寻找最大公约数。

理解原理：不仅仅满足于会做，更要理解每一步的原理，这样才能灵活运用。

七、相关问答FAQs

Q1: 为什么约分很重要？

A1: 约分很重要，因为它可以使分数更加简洁明了，便于比较大小和进行进一步的数学运算，最简形式的分数减少了不必要的复杂性，提高了数学表达的效率和准确性。

Q2: 如何快速找到两个数的最大公约数？

A2: 快速找到两个数的最大公约数可以使用辗转相除法（欧几里得算法），这是最常用且高效的方法，还可以使用在线最大公约数计算器或编程语言中的相关函数来快速求解。