详细指南与FAQs
在日常生活和学术研究中,我们经常需要计算一组数据的平均值,平均值是数据集中所有数值的总和除以数值的个数,它能够为我们提供数据集的中心趋势信息,本文将详细介绍如何求平均值,包括其定义、计算方法、不同类型数据的平均值计算以及相关的注意事项。
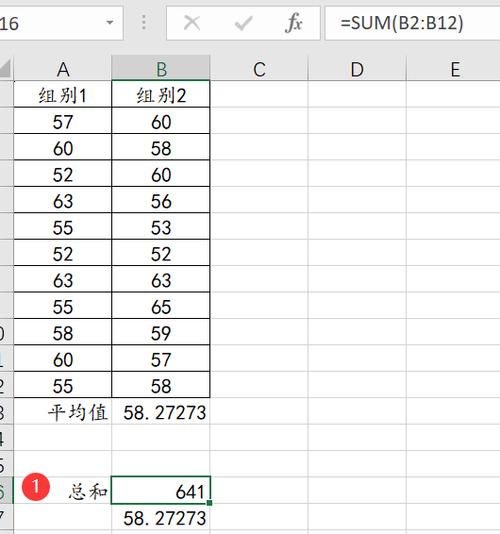
一、平均值的定义
平均值,也称为均值,是指一组数据中所有数据之和再除以这组数据的个数,它反映了数据的集中趋势,是统计学中最常用的统计量之一。
二、计算方法
(一)简单算术平均值
对于一组简单的数值数据,计算其平均值的步骤如下:
1、求和:将所有数据相加。
2、计数:确定数据的个数。

3、除法:用总和除以数据的个数。
有一组数据:2、4、6、8、10。
求和:2 + 4 + 6 + 8 + 10 = 30
计数:共有5个数据。
除法:30 ÷ 5 = 6
这组数据的平均值是6。
(二)加权平均值
当数据集中的不同数据具有不同的重要性或权重时,需要计算加权平均值,计算步骤如下:
1、确定权重:为每个数据分配相应的权重。
2、乘积求和:将每个数据与其对应的权重相乘,然后将所有乘积相加。
3、权重求和:将所有权重相加。
4、除法:用乘积的总和除以权重的总和。
某学生的考试成绩分别为80分(权重0.3)、90分(权重0.5)和70分(权重0.2)。
乘积求和:80×0.3 + 90×0.5 + 70×0.2 = 24 + 45 + 14 = 83
权重求和:0.3 + 0.5 + 0.2 = 1
除法:83 ÷ 1 = 83
该学生成绩的加权平均值是83分。
三、不同类型数据的平均值计算
(一)离散型数据
离散型数据是指只能取有限个或可数个值的数据,对于离散型数据,直接按照上述简单算术平均值或加权平均值的方法计算即可。
(二)连续型数据
连续型数据是指在一定范围内可以取任意值的数据,对于连续型数据,通常需要通过积分来计算平均值,但在实际应用中,我们常常通过对数据进行分组,将连续型数据近似看作离散型数据来计算平均值。
测量某地区居民的身高,身高是一个连续型数据,我们可以将身高划分为若干个区间,如150 160厘米、160 170厘米等,然后统计每个区间内的人数,再按照加权平均值的方法计算平均身高。
四、注意事项
1、数据的准确性:确保输入的数据准确无误,避免因数据错误导致平均值计算错误。
2、数据的代表性:选择的数据应具有代表性,能够反映数据集的整体特征,如果数据存在异常值,可能需要对异常值进行处理后再计算平均值。
3、选择合适的平均值类型:根据数据的特点和实际需求,选择合适的平均值类型,如果数据的重要性或权重不同,应使用加权平均值;如果数据是连续型数据且需要精确计算,可能需要采用积分的方法。
五、相关问答FAQs
问题1:平均值一定能够代表数据集的中心趋势吗?
答:不一定,平均值虽然能够反映数据集的中心趋势,但它容易受到极端值的影响,当数据集中存在极端值时,平均值可能无法准确代表数据的中心位置,中位数或众数可能是更好的选择,在一个班级中,大部分学生的成绩都在80分左右,但有一个学生的成绩只有20分,那么这个班级的平均成绩可能会比较低,不能很好地反映大多数学生的水平。
问题2:如何判断一组数据是否适合用平均值来描述其特征?
答:可以从以下几个方面来判断:一是数据是否具有同质性,即数据的性质和来源是否相似;二是数据是否没有明显的极端值;三是数据的分布是否大致对称,如果数据满足这些条件,那么用平均值来描述其特征是比较合适的,否则,可以考虑使用其他统计量,如中位数、众数或标准差等。