在数学中,最小公倍数(Least Common Multiple, LCM)是两个或多个整数共有的倍数中最小的一个,求最小公倍数的方法有多种,以下是几种常用的方法:
分解质因数法

1、步骤:
将每个数分解成质因数的乘积形式。
找出所有质因数中的最高次幂。
将这些最高次幂相乘,得到最小公倍数。
2、示例:求15和18的最小公倍数。
分解质因数:$15 = 3 \times 5$, $18 = 2 \times 3^2$。
找出最高次幂:$3^2$, $2$, $5$。
计算最小公倍数:$3^2 \times 2 \times 5 = 90$。
公式法
1、步骤:
先求出两个数的最大公约数(Greatest Common Divisor, GCD)。
使用公式:$\text{LCM}(a, b) = \frac{a \times b}{\text{GCD}(a, b)}$。

2、示例:求15和18的最小公倍数。
求最大公约数:$\text{GCD}(15, 18) = 3$。
使用公式:$\text{LCM}(15, 18) = \frac{15 \times 18}{3} = 90$。
短除法
1、步骤:
列出两个数的所有质因数。
找出公共质因数,并取每个质因数的最高次幂。
将所有最高次幂相乘,得到最小公倍数。
2、示例:求15和18的最小公倍数。
列出质因数:$15 = 3 \times 5$, $18 = 2 \times 3^2$。
找出公共质因数:$3$, $5$, $2$(注意只取一个3)。
计算最小公倍数:$3 \times 2 \times 5 = 30$。
扩大法
1、步骤:
如果两个数不是互质数,也没有倍数关系,可以将较大数依次扩大2倍、3倍...直到它成为较小数的倍数。
这个倍数就是最小公倍数。
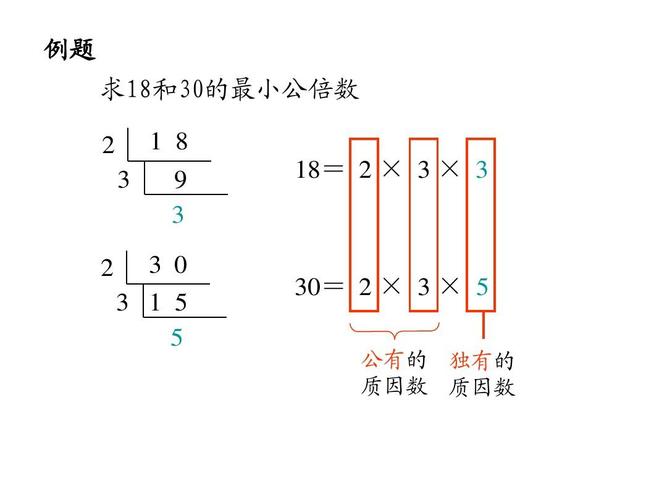
2、示例:求18和30的最小公倍数。
将30扩大2倍得60,60不是18的倍数;再扩大3倍得90,90是18的倍数。
18和30的最小公倍数是90。
两数相乘法
1、步骤:
如果两个数是互质数(即它们的最大公约数为1),那么它们的最小公倍数就是这两个数的乘积。
2、示例:求4和7的最小公倍数。
因为4和7是互质数,所以它们的最小公倍数是$4 \times 7 = 28$。
辗转相除法(用于求最大公约数)
1、步骤:
使用辗转相除法求出两个数的最大公约数。
然后使用公式法求出最小公倍数。
2、示例:求1997和615的最小公倍数。
使用辗转相除法求最大公约数:$\text{GCD}(1997, 615) = 1$。
使用公式法:$\text{LCM}(1997, 615) = \frac{1997 \times 615}{1} = 1235505$。
通过以上方法,可以有效地求出任意两个或多个整数的最小公倍数,每种方法都有其适用的场景,选择合适的方法可以简化计算过程。
FAQs
问题1:如何快速判断两个数是否互质?
解答:如果两个数的最大公约数为1,那么这两个数就是互质的,可以通过辗转相除法或者更相减损术来判断,4和7的最大公约数为1,因此它们是互质的。
问题2:当两个数有倍数关系时,如何快速求它们的最小公倍数?
解答:如果两个数有倍数关系,较大的数就是这两个数的最小公倍数,3和15有倍数关系,因此它们的最小公倍数是15。











