分位数是一种统计量，它表示一组数据中某个特定百分位的数值，中位数（即二分位数）是将所有数据从小到大排序后位于中间位置的值；四分位数是将数据分为四等份后的三个分割点位置的数值，以下是分位数计算方法的具体介绍：

1、确定分位数

定义：分位数是指将一个随机变量的概率分布范围分为几个等份的数值点，常用的有中位数（即二分位数）、四分位数、百分位数等。

计算方法：对于二分位数，也就是中位数，可以通过把所有观察值高低排序后，找出正中间的一个作为中位数，注意观察法适用于有限的数集，如果观察值有偶数个，则中位数不唯一，通常取最中间的两个数值的平均数作为中位数。

2、计算四分位数

定义：四分位数（Quartiles）包括第一四分位数（Q1，又称下四分位数），第二四分位数（Q2，又称中位数）和第三四分位数（Q3，又称上四分位数），四分位数在统计学中的箱线图绘制上具有重要作用。

手工计算方法：将数据按从小到大的顺序排列，然后计算出每个数据的百分位数，即每个数据在整个数据集中的百分比，根据百分位数，计算出每个数据的分位数，如果一组数据有10个数据，那么第一个数据的百分位数就是10%，第二个数据的百分位数就是20%，以此类推，最后一个数据的百分位数就是100%。

具体计算步骤：先将数据从小到大排序，计算p分位数的位置公式为position = 1 + (n1)*p，其中n为数据长度，确定p分位数处的具体数值，如果该位置处于两个数据之间，则通过插值计算得到该位置的数值。

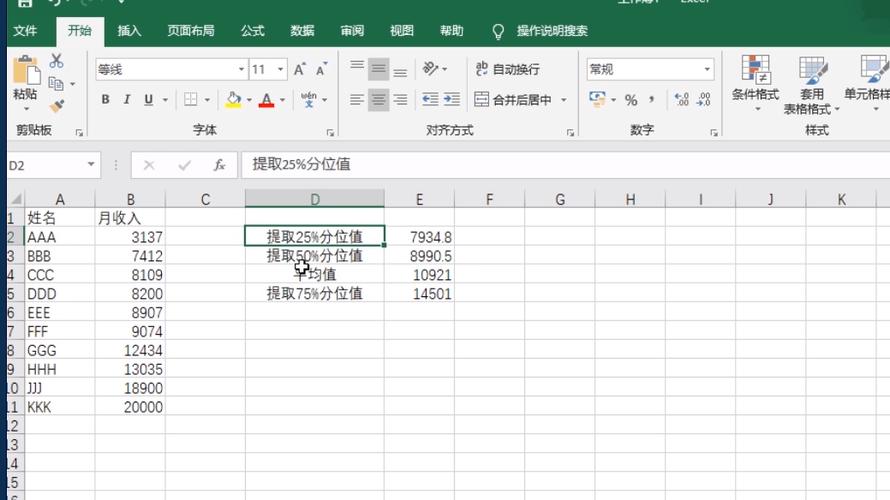
3、应用举例

实例一：给出一组数据before_data：6, 47, 49, 15, 42, 41, 7, 39, 43, 40, 36，一共11项，从小到大排序后结果data：6, 7, 15, 36, 39, 40, 41, 42, 43, 47, 49，计算Q1、Q2、Q3分别为15、40、43.5。

实例二：给出一组数据before_data：7, 15, 36, 39, 40, 41,20,18，一共8项，从小到大排序后结果data：7,15,18,20,36,39,40,41，计算Q1、Q2、Q3分别为17.25、28、42.5。

分位数是一种重要的统计量，用于描述数据的分布特征，通过掌握分位数的计算方法和应用场景，可以更好地理解和分析数据。