要证明四个点共面,可以通过几何和代数方法进行,以下是详细的步骤:
1、向量法:
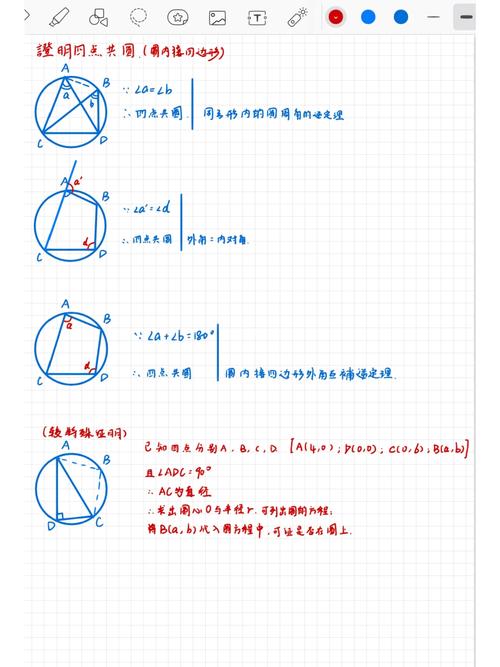
假设四个点为A、B、C、D,选择其中三个点(例如A、B、C)构造两个向量\[ \vec{AB} = \vec{B} \vec{A} \]和\[ \vec{AC} = \vec{C} \vec{A} \]。
利用向量加法,构造第三个向量\[ \vec{AD} = x \vec{AB} + y \vec{AC} \],其中x和y是实数对,且满足x+y=1。
检查第四点D是否在向量\[ \vec{AD} \]上,即验证\[ D = P + x(B A) + y(C A) \],如果满足这个条件,则四点共面。
2、行列式法:
设四个点的坐标分别为O(x0, y0, z0)、A(x1, y1, z1)、B(x2, y2, z2)、C(x3, y3, z3)。
构造向量\[ \vec{OA} = (x1 x0, y1 y0, z1 z0) \]、\[ \vec{OB} = (x2 x0, y2 y0, z2 z0) \]和\[ \vec{OC} = (x3 x0, y3 y0, z3 z0) \]。
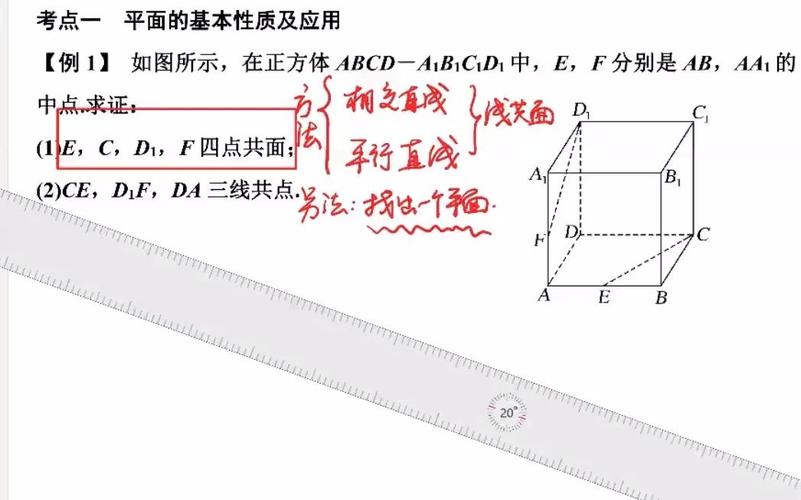
计算这三个向量的行列式,如果行列式的值为0,则表示这些向量共面,即四点共面。
3、共面向量定理:
假设有四个点A、B、C、D,选择其中一个点O作为参考点。
计算向量\[ \vec{OA} \]、\[ \vec{OB} \]、\[ \vec{OC} \]。
如果存在实数a、b、c使得\[ a + b + c = 1 \][ \vec{OD} = a \vec{OA} + b \vec{OB} + c \vec{OC} \],则四点共面。
通过上述任一方法,可以有效地判断四个点是否共面,这些方法不仅适用于理论上的证明,也可以应用于实际问题的解决,如计算机图形学、机器人路径规划等领域。