圆的面积计算是一个基本的几何问题,涉及到圆周率、半径和直径等概念,以下将详细解释圆的面积计算公式、推导过程以及相关的应用:
1、圆面积公式
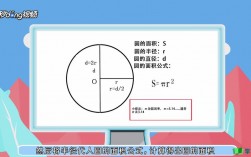
基本公式:圆的面积 \( S \) 可以通过半径 \( r \) 或直径 \( d \) 来计算,标准公式为 \( S = \pi r^2 \),\( \pi \) 是圆周率,其值约为3.1415926,另一个常用公式是 \( S = \frac{\pi d^2}{4} \)。
半圆面积:如果只需计算半圆的面积,可以将整个圆的面积除以2,即 \( S_{\text{半圆}} = \frac{\pi r^2}{2} \)。
圆环面积:对于圆环(即两个同心圆之间的区域),其面积可以通过大圆面积减去小圆面积来计算:\( S_{\text{圆环}} = \pi (R^2 r^2) \),\( R \) 是大圆半径,\( r \) 是小圆半径。
2、公式推导
几何法:将圆分割成若干小扇形,每个小扇形可以近似看作一个三角形,随着分割次数的增加,这些小扇形的总面积趋近于圆的面积,通过积分方法,可以得到圆面积的精确值为 \( \pi r^2 \)。
代数法:利用圆的周长公式 \( C = 2\pi r \),可以将圆看作一个长方形,其宽为半径 \( r \),长为圆周长的一半 \( \pi r \),圆的面积 \( S = r \times \frac{C}{2} = r \times \pi r = \pi r^2 \)。

3、相关计算工具
有许多在线工具可以帮助快速计算圆的面积、周长、直径等,圆形计算器允许用户输入已知变量(如半径、直径、周长)并计算出其他未知变量。
使用这些工具时,只需输入相应的数值并选择计算类型,即可得到结果,输入半径后,工具会自动计算出圆的面积、周长和直径。
4、实际应用
工程设计:在土木工程中,计算圆形地基或管道的截面积是常见的任务。
科学研究:物理学和工程学中的许多问题都涉及到圆的面积计算,如流体动力学中的管道流量计算。

教育领域:作为基础数学教育的一部分,圆的面积计算帮助学生理解几何概念和数学原理。
5、注意事项
单位一致性:在计算过程中,确保所有单位一致,如果半径以米为单位,那么计算出的面积应以平方米为单位。
精度要求:根据实际需要选择合适的π值,一般计算中使用3.14已经足够,但对于高精度要求的情况,应使用更多位数的π值。
特殊情况处理:对于半径为零或负值的情况,应特别小心,因为这些情况下圆的面积为零或无意义。
圆的面积计算是一个简单但重要的几何问题,通过理解和掌握相关公式和方法,可以有效地解决实际问题。