圆的面积计算是几何学中的基本问题之一,其计算公式为S=πr²或S=π(d/2)²,表示圆周率,通常取值为3.14;r表示半径;d表示直径,以下是具体介绍:
圆面积公式及其推导
1、基本公式:圆面积的基本公式为S=πr²,这个公式表明,圆的面积等于圆周率乘以半径的平方,如果已知圆的直径d,则可以通过将直径除以2得到半径,即r=d/2,再代入公式计算面积。
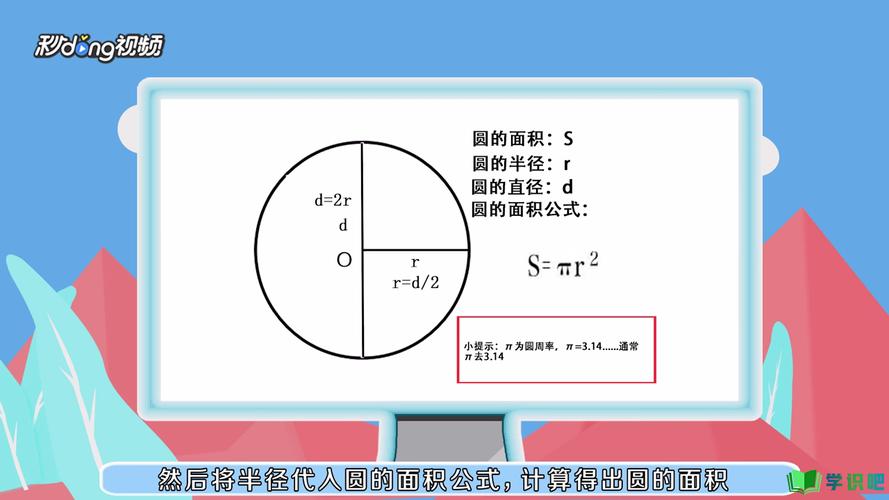
2、公式推导:圆面积公式的推导有多种方法,其中一种常见的方法是将圆分割成无数个小扇形,然后近似地将这些小扇形拼成一个长方形,长方形的长就是圆周长的一半,宽就是圆的半径,长方形的面积(即圆的面积)可以表示为长乘以宽,即C/2×r,由于C=2πr,所以最终得到S=πr²。
计算方法及示例
1、利用半径计算:如果题目给出了圆的半径长度,可以直接代入公式S=πr²进行计算,一个圆的半径为5厘米,那么其面积为S=π×5²≈78.54平方厘米(取π≈3.14)。
2、利用直径计算:如果题目给出了圆的直径长度,可以先根据直径计算出半径(r=d/2),再代入公式计算面积,一个圆的直径为10厘米,那么其半径为5厘米,面积同样为S=π×5²≈78.54平方厘米。
3、利用周长计算:如果题目给出了圆的周长,可以先根据周长公式C=2πr计算出半径(r=C/(2π)),再代入面积公式计算面积,一个圆的周长为31.4厘米,那么其半径为31.4/(2×3.14)≈5厘米,面积为S=π×5²≈78.54平方厘米。
特殊情况及应用
1、半圆面积:半圆的面积是整个圆面积的一半,如果一个圆的半径为r,那么半圆的面积为S半圆=(πr²)/2。
2、圆环面积:圆环是由两个同心圆组成的区域,圆环的面积等于大圆面积减去小圆面积,即S大圆S小圆=π(R²r²),其中R为大圆半径,r为小圆半径。

3、实际应用:圆面积的计算在现实生活中有广泛的应用,如计算圆形花园的面积、圆形水池的容量等,通过掌握圆面积的计算公式和计算方法,可以方便地解决这些实际问题。
相关问答FAQs
1、问:如果只知道圆的周长,如何计算其面积?
答:如果只知道圆的周长C,可以根据周长公式C=2πr计算出半径r(r=C/(2π)),再代入面积公式S=πr²计算面积。
2、问:如何计算半圆的面积?
答:半圆的面积是整个圆面积的一半,如果一个圆的半径为r,那么半圆的面积为S半圆=(πr²)/2。
通过以上步骤和示例,可以清晰地理解并掌握如何计算圆的面积,在实际应用中,只需根据已知条件选择合适的公式和方法进行计算即可。