圆的周长是指绕圆一周的长度,也被称为圆的circumference,计算圆的周长是几何学中的一个基础而重要的任务,它不仅在数学中有着广泛的应用,还在物理学、工程学等领域中发挥着重要作用。
一、基本概念与公式
1、圆的定义:
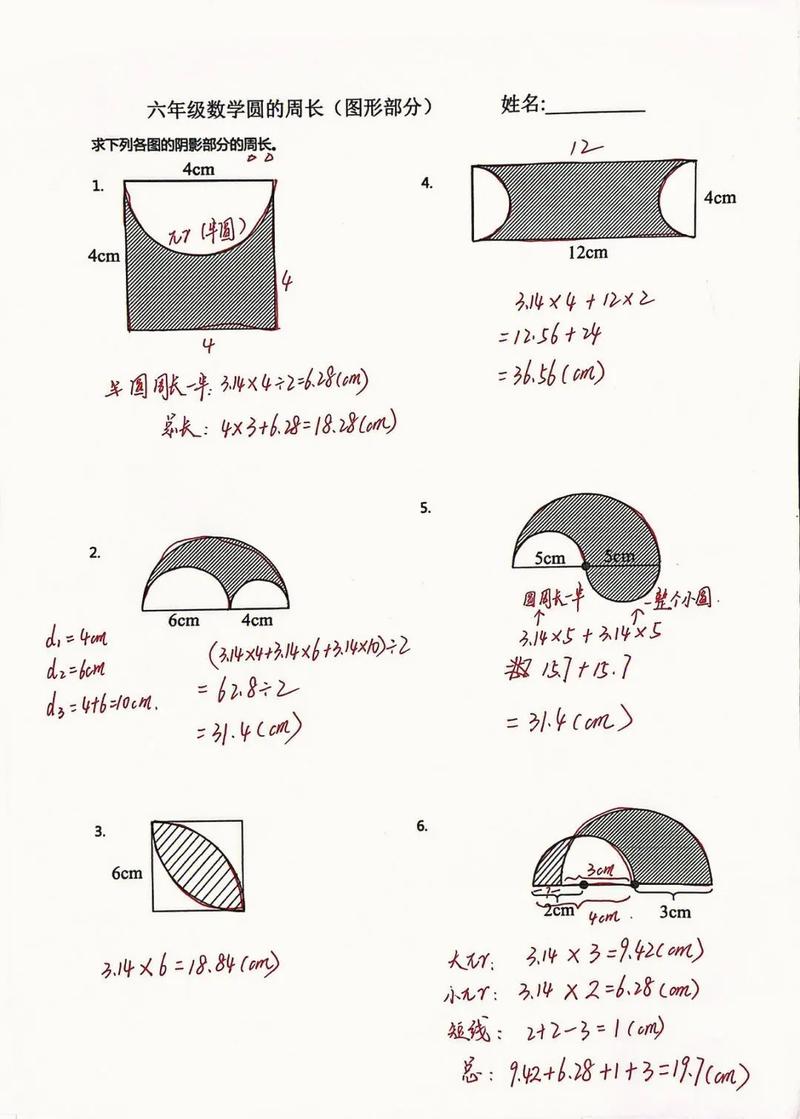
圆是一个二维平面上的形状,由一个固定点(圆心)与等距离该点的所有点组成。
圆周是圆的边界,而圆的半径是从圆心到圆周上任意一点的距离。
圆的直径是穿过圆心的一条线段,其两端分别位于圆周上,等于半径的两倍。
2、圆周率(π):
圆周率是一个无理数,表示圆的周长与其直径的比例,通常用希腊字母π表示,其值约为3.14159。
π的值在数学和物理中具有极其重要的地位,是精确计算圆周长、圆面积、球体积等几何形状的关键值。

3、周长公式:
如果已知圆的直径d,则圆的周长C可以通过公式C = πd计算得出。
如果已知圆的半径r,则圆的周长C可以通过公式C = 2πr计算得出。
二、计算步骤与示例
1、确定已知量:
首先需要知道圆的直径或半径,这两个量是计算圆周长的基础。
2、选择公式:
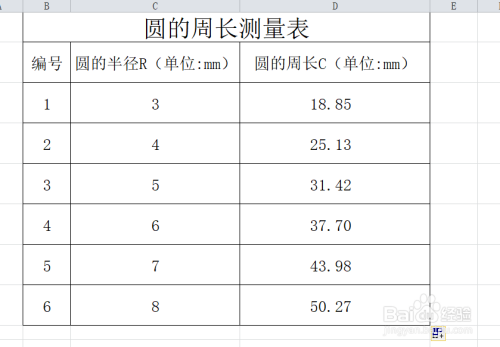
根据已知量选择合适的公式进行计算,如果已知直径,则使用C = πd;如果已知半径,则使用C = 2πr。
3、代入数值:
将已知数值代入所选公式中进行计算,如果已知半径为5厘米,则周长C = 2 × π × 5 = 10π厘米。
4、近似值处理:
由于π是一个无理数,其小数部分无限不循环,因此在实际应用中通常会使用π的近似值进行计算,可以使用3.14或更精确的3.14159等值来代替π进行计算。
5、示例:
例1:假设一个圆的直径为10厘米,求其周长,根据公式C = πd,代入数值得到C = π × 10 ≈ 31.4159厘米(取π ≈ 3.14159)。
例2:假设一个圆的半径为7厘米,求其周长,根据公式C = 2πr,代入数值得到C = 2 × π × 7 ≈ 43.9823厘米(取π ≈ 3.14159)。
三、注意事项
1、单位一致性:
在计算过程中,务必保持单位一致,如果直径或半径以厘米为单位,则计算出的周长也应为厘米。
2、精度要求:
根据实际需求选择合适的π值精度,对于一般计算,使用3.14即可;对于高精度计算,应使用更多位数的π值。
3、应用场景:
圆的周长计算在日常生活和科学研究中都有广泛应用,在制造轮胎、设计圆形容器、计算天体运行轨道等方面都需要用到圆周长的计算。
四、相关问答FAQs
问1:如何计算圆的周长?
答:圆的周长可以通过公式C = πd(如果已知直径)或C = 2πr(如果已知半径)来计算,是圆周率,其值约为3.14159;d是圆的直径;r是圆的半径。
问2:为什么使用π来计算圆的周长?
答:因为π是圆的周长与直径的比例常数,无论圆的大小如何变化,这个比例始终保持不变,通过乘以π并考虑直径或半径的变化,我们可以准确地计算出任何大小圆的周长。π的存在使得我们能够以一种统一且精确的方式描述和计算圆的几何特性。
掌握圆的周长计算方法对于学习几何和解决实际问题都具有重要意义,通过理解基本概念、熟悉计算公式并注意相关事项,我们可以准确计算出任何圆的周长。