如何算平均数

一、定义和基本概念

平均数是统计学中最基本、最常用的一种指标，用于描述一组数据的一般水平，它能够消除个体标志值之间的差异，体现出总体的一般特征，根据计算方法的不同，平均数可以分为算术平均数、调和平均数、几何平均数和位置平均数等。

二、算术平均数

算术平均数是最常见的平均数类型，其计算公式为：

\[ \text{算术平均数} = \frac{\sum_{i=1}^{n} x_i}{n} \]

\( x_i \) 表示第 \( i \) 个数据点，\( n \) 表示数据点的总数。

1.简单算术平均数

适用于未分组的原始数据，若一组数据为 \( X_1, X_2, ..., X_n \)，则其简单算术平均数为：

\[ \bar{X} = \frac{X_1 + X_2 + ... + X_n}{n} \]

2.加权算术平均数

主要用于处理经分组整理的数据，设原始数据被分成 \( K \) 组，各组的组中值为 \( X_1, X_2, ..., X_k \)，各组的频数分别为 \( f_1, f_2, ..., f_k \)，则加权算术平均数的计算公式为：

\[ \bar{X} = \frac{\sum_{i=1}^{k} (X_i \cdot f_i)}{\sum_{i=1}^{k} f_i} \]

3.应用场景

适用于数值型数据，不适用于品质数据，常用于分析总体的一般特征。

4.特点

反应灵敏、确定严密、简明易解、计算简单、适合进一步演算和较小抽样变化的影响。

但极易受极端数据的影响，每个数据的或大或小的变化都会影响最终结果。

三、调和平均数

调和平均数是算术平均数的变形，其计算公式为：

\[ H = \frac{n}{\sum_{i=1}^{n} \frac{1}{x_i}} \]

\( x_i \) 表示第 \( i \) 个数据点，\( n \) 表示数据点的总数。

1.简单调和平均数

适用于未分组的原始数据，若一组数据为 \( X_1, X_2, ..., X_n \)，则其简单调和平均数为：

\[ H = \frac{n}{\sum_{i=1}^{n} \frac{1}{X_i}} \]

2.加权调和平均数

主要用于处理经分组整理的数据，设原始数据被分成 \( K \) 组，各组的组中值为 \( X_1, X_2, ..., X_k \)，各组的频数分别为 \( f_1, f_2, ..., f_k \)，则加权调和平均数的计算公式为：

\[ H = \frac{\sum_{i=1}^{k} f_i}{\sum_{i=1}^{k} \frac{f_i}{X_i}} \]

3.应用场景

可以用于计算平均速度，如在计算4x100米接力赛中运动员的总体速度时使用。

4.特点

易受极端值的影响，且受极小值的影响比受极大值的影响更大。

只要有一个标志值为0，就不能计算调和平均数。

当组距数列有开口组时，其组中值即使按照相邻组距计算，假定性也很大。

应用的范围较小。

四、几何平均数

几何平均数是对各变量值的连乘积开项数次方根，其计算公式为：

\[ G = \left( \prod_{i=1}^{n} x_i \right)^{\frac{1}{n}} \]

\( x_i \) 表示第 \( i \) 个数据点，\( n \) 表示数据点的总数。

1.简单几何平均数

适用于未分组的原始数据，若一组数据为 \( X_1, X_2, ..., X_n \)，则其简单几何平均数为：

\[ G = \left( X_1 \cdot X_2 \cdot ... \cdot X_n \right)^{\frac{1}{n}} \]

2.加权几何平均数

主要用于处理经分组整理的数据，设原始数据被分成 \( K \) 组，各组的组中值为 \( X_1, X_2, ..., X_k \)，各组的频数分别为 \( f_1, f_2, ..., f_k \)，则加权几何平均数的计算公式为：

\[ G = \left( \prod_{i=1}^{k} X_i^{f_i} \right)^{\frac{1}{\sum_{i=1}^{k} f_i}} \]

3.应用场景

对比率、指数等进行平均。

计算平均发展速度。

复利下的平均年利率。

连续作业的车间产品的平均合格率。

4.特点

受极值影响较算术平均数小。

不能有零和负值。

五、位置平均数

位置平均数是指特殊位置上的数据作为代表值，常用的位置平均数有中位数和众数。

1.中位数

中位数是将一组数据按从小到大的顺序排列后居于中间位置的数值，对于奇数个数据，中位数是正中间的那个数；对于偶数个数据，中位数则是中间两个数的平均数。

2.众数

众数是一组数据中出现次数最多的数值，在离散型数据中使用较多。

3.应用场景与特点

中位数不受极值影响，缺乏敏感性。

众数也不受极值影响，但当数据均匀分布时无众数。

皮尔逊经验指出，众数与算术平均数的距离约为中位数与算术平均数距离的3倍。

六、Excel中的计算方法

在Excel中，有多种方法可以计算平均数，包括使用公式、函数和数据工具，以下是几种常用的方法：

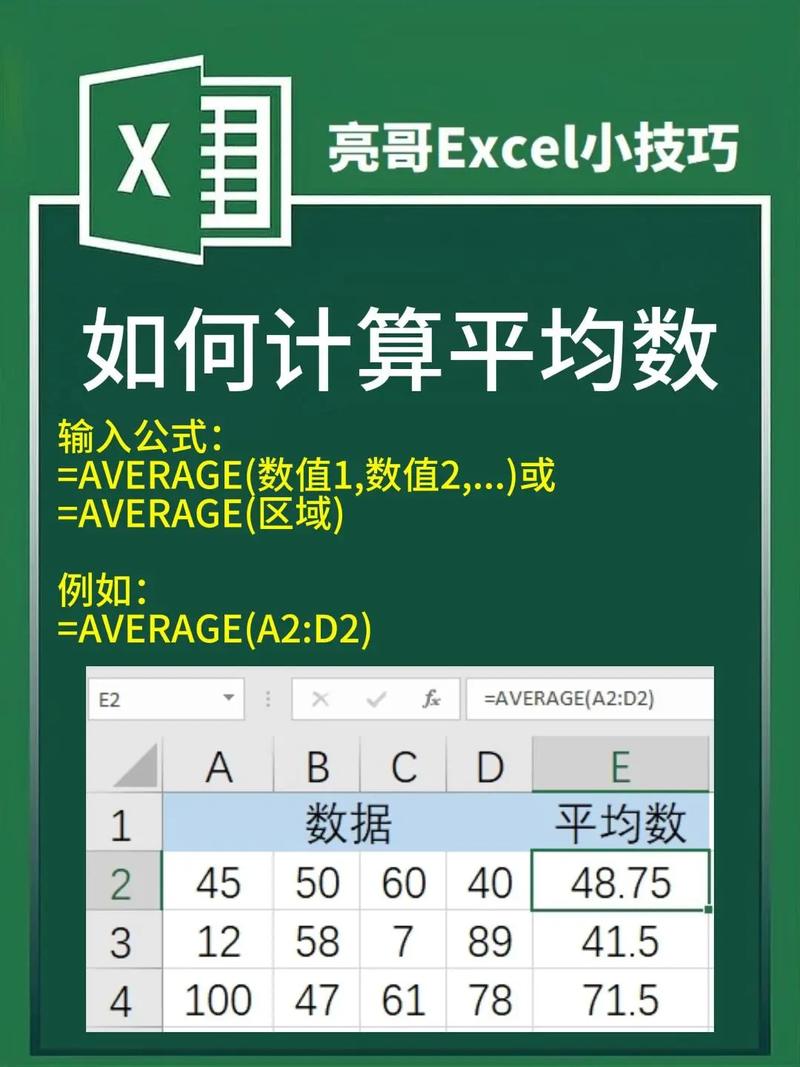
1.使用AVERAGE函数

这是最简单的方法，通过AVERAGE函数可以快速计算一组数据的平均值，如果你的数据在A1到A10单元格中，可以使用以下公式：

=AVERAGE(A1:A10)

AVERAGE函数会自动忽略空单元格和文本单元格，只计算数值单元格的平均值，这使得它非常方便和高效，特别是在处理大型数据集时。

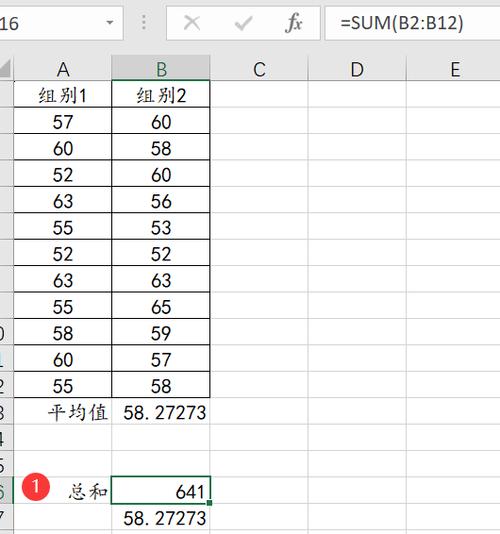
2.使用SUM和COUNT函数结合

你可能需要更灵活的方式来计算平均值，这时可以结合使用SUM和COUNT函数，SUM函数计算数据的总和，COUNT函数计算数据的数量，将总和除以数量即得到平均值。

=SUM(A1:A10)/COUNT(A1:A10)

这种方法的好处是你可以更容易地控制和修改公式，适用于需要自定义计算的场景。

3.使用SUBTOTAL函数

SUBTOTAL函数是一个更高级的工具，特别适用于有筛选条件的数据集，SUBTOTAL函数不仅可以计算平均值，还可以计算其他统计量（如总和、计数等），假设你有一个已经筛选的数据表，可以使用以下公式计算筛选后数据的平均值：

=SUBTOTAL(101, A1:A10)

这里，101表示计算平均值，A1:A10是数据范围，SUBTOTAL函数会自动忽略被筛选掉的行。

4.使用数据透视表

数据透视表是Excel中非常强大的工具，可以帮助你快速汇总和分析数据，在数据透视表中，可以轻松计算不同条件下的数据平均值，选择数据源，然后插入数据透视表，在数据透视表中，将需要计算平均值的字段拖到“值”区域，并选择“平均值”作为汇总方式。

在选择计算平均数的方法时，应根据数据的特点和分析需求来确定最合适的方法，以下是一些建议：

如果数据集中没有极端值，且数据较为均匀分布，可以选择算术平均数。

如果数据中存在极端值，且这些极端值对整体趋势影响不大，可以考虑使用中位数或众数来描述数据的一般水平。

如果需要计算比率或比例的平均值，或者处理复利下的平均年利率等问题时，应使用几何平均数。

在Excel中处理数据时，可以利用内置函数和工具来简化计算过程，提高工作效率和准确性，特别是对于大型数据集或需要频繁更新的数据来说，使用数据透视表等工具可以更加方便地进行数据分析和汇总。