开平方是数学中常见的一种运算,用于求一个数的平方根,本文将详细介绍开平方的方法和原理,帮助大家更好地理解和掌握这一运算。
一、定义与理论基础
开平方是一种数学运算,用于求解一个数a的平方根,记作√a,根据平方的定义,如果y² = a,那么y就是a的平方根,在实数范围内,只有非负数才有平方根。
二、简单平方数开平方方法
对于简单的平方数,如196、2025、121等,我们可以通过直接观察或简单的计算得出其平方根。
196 = 14²,196 = 14。
2025 = 45²,2025 = 45。
121 = 11²,121 = 11。
这种方法适用于那些能够直接分解为某个整数平方的数。
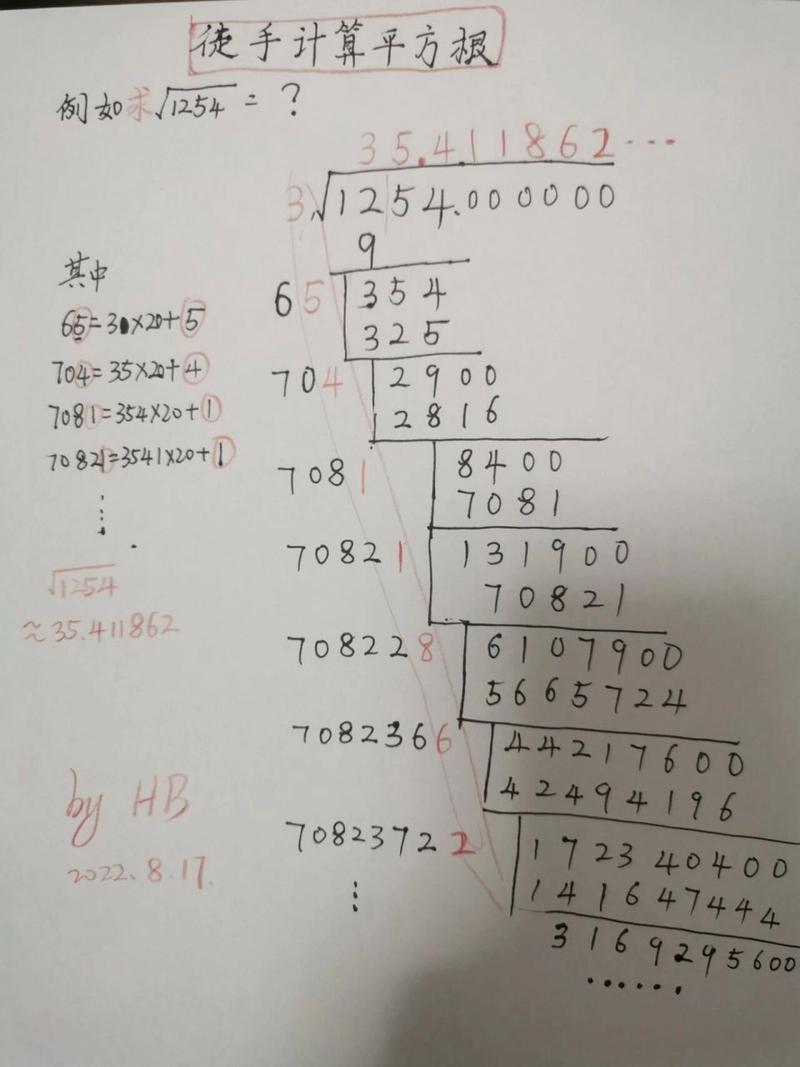
三、手撕平方法(适用于高中阶段)
对于不能直接开出整数平方根的数,我们可以采用手撕平方法进行近似计算,这种方法特别适用于考试中的快速估算,以下是手撕平方法的步骤:
1、定头部:从个位数开始,往左边数,每次数两个数,每两个数分一组,对于151.29,分组后为1'51.29,头部是1。
2、定开方首数:由于1² = 1,所以由头部确定的开方首数是1。
3、试商:使用特定的试商规则进行计算,将开方首数乘以20,然后加上某个个位数字后再乘以该个位数字,以该个位数字作为商,如果余数不为零,继续掉落两个数字进行重复操作,直到得到需要的结果为止,最后的商即为所求的平方根。
需要注意的是,这种方法虽然简便快捷,但结果可能存在一定的误差。
四、笔算开平方方法(竖式除法)
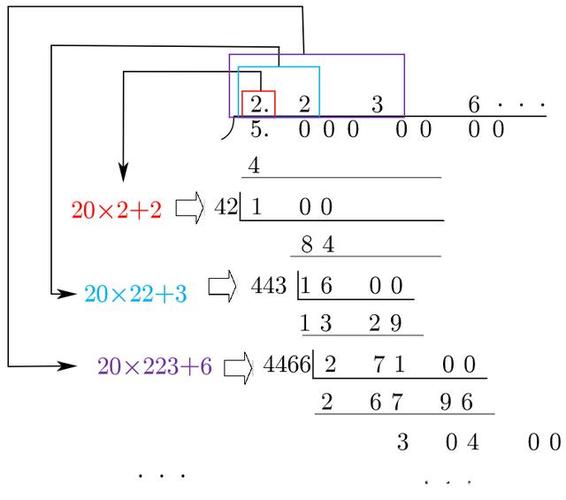
笔算开平方是一种更为精确的计算方法,特别适用于需要任意精确度的平方根计算,以下是笔算开平方的步骤:
1、分段:将被开方数的整数部分从个位起向左每隔两位划为一段,用撇号分开,对于1234,分段后为1,23|4。
2、试根:根据左边第一段里的数,求得平方根的最高位上的数,对于1234,最高位上的数为3(因为3²=9最接近12)。
3、求余项:从第一段的数减去最高位上数的平方,在它们的差的右边写上第二段数组成第一个余数,对于1234,第一个余数为256(即129²=3,再将3与第二段的4组合成34)。
4、更新余项:把求得的最高位数乘以20去试除第一个余数,所得的最大整数作为试商,然后用所求的平方根的最高位数的20倍加上这个试商再乘以试商,如果所得的积小于或等于余数,试商就是平方根的第二位数;如果所得的积大于余数,就把试商减小再试。
5、重复:用同样的方法继续求平方根的其他各位上的数。
这种方法虽然计算过程较为繁琐,但可以得到非常精确的结果。
五、连分数法与长除法
除了上述方法外,还有连分数法和长除法等其他开平方方法,这些方法各有优缺点和适用范围,可以根据具体需求选择合适的方法进行计算。
六、实例演示
为了更直观地展示开平方的过程,下面以一个具体实例进行演示:
假设我们要计算√3592的值。
1、分段:3592可以分段为3,59|2。
2、试根:最高位上的数为5(因为5²=25最接近35)。
3、求余项:从35中减去25得到余数10,再将10与第二段的92组合成1092。
4、更新余项:将5乘以20得到100,然后用100去试除1092,经过计算发现4是最合适的试商(因为4²=16且16小于1092)。
5、重复:将5×20+4=104作为新的除数去试除109216=1076,经过计算发现3是最合适的试商(因为3²=9且9小于1076)。
6、继续:以此类推,直到得到足够精确的结果为止,最终我们可以得到√3592≈59.9(保留一位小数)。
七、注意事项
在进行开平方运算时,要注意被开方数必须是非负数。
不同的开平方方法有不同的适用范围和精度要求,应根据实际需求选择合适的方法。
在笔算开平方过程中,要注意每一步的计算准确性和逻辑清晰性。
八、相关问答FAQs
Q1: 如果碰到小数点怎么开平方?
A1: 如果碰到小数点,只需在商的小数点对齐被开方数的小数点即可,对于0.26这样的小数,我们可以将其视为26×10⁻²进行开方计算。
Q2: 如果遇到纯小数或者最简分数又该怎样开平方呢?
A2: 对于纯小数或最简分数的开平方,可以先将它们转换为十进制形式或通过适当的变换使其适合上述开平方方法的应用范围,对于最简分数可以通过乘方的方式转化为适合开平方的形式,对于纯小数则可以直接应用上述方法进行计算。
通过以上介绍可以看出开平方运算并不复杂只要掌握了正确的方法和技巧就可以轻松应对各种开平方问题了,希望本文能够帮助大家更好地理解和掌握开平方这一重要的数学运算。