开根号是数学中一个基本且常用的操作,无论是在日常生活中还是在科学研究中,都经常需要计算一个数的平方根,以下是一些关于如何开根号的方法:
使用计算器开根号
1、科学计算器:科学计算器通常设有单独的“√”键,用于直接计算平方根,用户只需输入被开方数,然后按下“√”键,屏幕上即会显示结果。
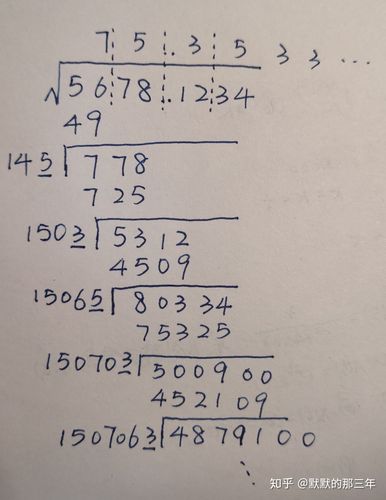
2、函数计算器:对于没有独立根号键的函数计算器,可以通过输入函数表达式或利用幂运算来开根号,可以输入“√(x)”或“x^(1/2)”来计算平方根。
3、简易计算器:简易计算器可能没有专门的根号键,但可以通过多次平方根运算逼近结果,要求解√123,可以先输入123,然后反复按"√"键,直到结果足够精确。
手算开根号(以竖式手算为例)
1、确定首位数字:找出自乘后依然小于目标数的最大正整数作为求根的第一步结果,求√3时,首位数字为1。
2、逐步逼近:将当前结果的两倍作为过渡值,补上适当的个位数字,使其与过渡值的乘积尽量接近目标数,然后从目标数中减去该乘积,得到下一步的误差值。
3、重复操作:继续用新的过渡值和误差值进行操作,直到达到所需的精度,每次操作都会得到一位新的有效数字。
因式分解法开根号
1、完全平方数:如果被开方数是完全平方数,可以直接去掉根号,换成平方根数。√121 = 11。

2、完全立方数:如果被开方数是完全立方数,可以直接去掉根号,换成立方根数。√512 = 8。
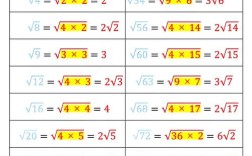
3、因式分解:将被开方数拆成乘数的组合,直到有完全平方数为止。√45 = √(9×5) = 3√5。
近似估算法
1、线性部分逼近:通过求出整数部分和小数部分的线性逼近来估算平方根,求√12时,可以先求出其整数部分3,然后求小数部分的近似值。
2、误差缩小:通过多次乘以100或1000等因子来缩小误差,提高逼近的精度,这种方法适用于快速估算,但精度有限。
开根号可以通过多种方法实现,包括使用计算器、手算、因式分解以及近似估算,每种方法都有其适用场景和优缺点,可以根据具体需求选择合适的方法,在实际操作中,应注意检查计算器模式、处理负数开方的情况,并确保计算的准确性和有效性。