开方是数学中常见的运算之一,它用于找到一个数的平方根或立方根等,我们将详细介绍如何进行开方运算,包括平方根和立方根的求解方法。
一、平方根的定义与性质
定义: 一个数 \( x \) 的平方根是一个数 \( y \),使得 \( y^2 = x \),通常用符号 \(\sqrt{x}\) 表示 \( x \) 的平方根。

性质:
1、非负性: 对于任何实数 \( x \),其平方根总是非负的。
2、唯一性: 每个非负实数有且只有一个正平方根。
3、乘法性质: \(\sqrt{a} \times \sqrt{b} = \sqrt{ab}\)。
4、除法性质: \(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\)(前提是 \( b > 0 \))。
二、平方根的计算方法
1. 手工计算
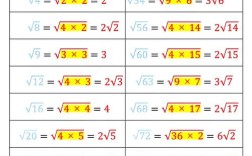
完全平方数: \( x \) 是一个完全平方数,\( x = 9 \),则 \(\sqrt{x} = 3\)。
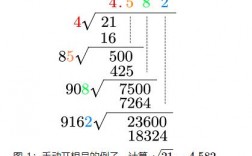
试错法: 对于不是完全平方数的情况,可以通过试错法找到近似值,求 \(\sqrt{50}\):
首先找到一个接近50的完全平方数,这里是49 (\(7^2\))。
然后逐步增加或减少这个数,直到找到最接近50的数,\(\sqrt{50} \approx 7.07\)。
2. 使用计算器
大多数科学计算器都有开方功能,直接输入需要开方的数字后按下开方键即可得到结果。

3. 牛顿迭代法
这是一种数值方法,用于精确计算平方根,步骤如下:
选择一个初始猜测值 \( g_0 \)(通常可以从完全平方数开始)。
使用公式 \( g_{n+1} = \frac{1}{2} \left( g_n + \frac{x}{g_n} \right) \) 进行迭代,直到两次迭代的结果足够接近为止。
三、立方根的定义与性质
定义: 一个数 \( x \) 的立方根是一个数 \( y \),使得 \( y^3 = x \),通常用符号 \(\sqrt[3]{x}\) 或 \( x^{1/3} \) 表示 \( x \) 的立方根。
性质:
1、实数范围内的连续性: 对于所有实数 \( x \),都存在唯一的实数立方根。
2、符号规则: \( x > 0 \),则 \(\sqrt[3]{x} > 0\);\( x < 0 \),则 \(\sqrt[3]{x} < 0\);\( x = 0 \),则 \(\sqrt[3]{x} = 0\)。
四、立方根的计算方法
1. 手工计算
完全立方数: \( x \) 是一个完全立方数,\( x = 8 \),则 \(\sqrt[3]{x} = 2\)。
试错法: 对于不是完全立方数的情况,可以通过试错法找到近似值,求 \(\sqrt[3]{27}\):
首先找到一个接近27的完全立方数,这里是26 (\(3^3\))。
然后逐步增加或减少这个数,直到找到最接近27的数,\(\sqrt[3]{27} \approx 3\)。
2. 使用计算器
大多数科学计算器也有立方根功能,直接输入需要开立方的数字后按下相应的开立方键即可得到结果。
3. 牛顿迭代法
同样适用于立方根的计算,只需将上述平方根迭代公式中的指数改为3即可。
五、表格示例
| 数字 | 平方根 (手工估算) | 平方根 (计算器) | 立方根 (手工估算) | 立方根 (计算器) |
| 25 | 5 | 5 | ||
| 50 | 7.07 | 7.071 | ||
| 27 | 3 | 3 | ||
| 8 | 2 | 2 |
六、FAQs
Q1: 如何判断一个数是否有平方根?
A1: 只有当一个数是非负数时,它才有实数范围内的平方根,负数没有实数平方根,但有复数平方根。
Q2: 为什么有时候计算器上的平方根结果是负数?
A2: 这是由于计算器的默认设置可能允许负数作为输入,而输出的是该负数的正平方根,负数没有实数平方根,所以这种情况下应该检查输入是否正确。