根号如何计算
根号,这一数学符号如同开启数学之门的一把钥匙,它代表着对数值进行开方运算的深邃操作,是初等数学教育中不可或缺的重要组成部分,从最直观的平方根概念出发,逐步深入至立方根乃至更高次方根的理解与应用,根号不仅丰富了数学的表达体系,更为解决实际问题提供了强有力的工具,通过探讨根号的计算方法、应用场景以及与其他数学概念的关联,我们可以更加深刻地理解数学的内在逻辑与美感,感受到其在推动科技进步与社会发展中的重要作用。

根号的定义与基本性质
1. 定义
根号,又称方根符号,用于表示对一个数进行开方运算,最常见的是二次方根,即平方根,用符号√表示。√4=2,表示4的平方根是2,还有三次方根(立方根),用符号³√表示,以及更高次方根。
2. 基本性质
非负性:一个非负数的平方根是非负数。
唯一性:在实数范围内,每个非负数有且只有一个正平方根。
乘法分配率:√(a*b) = √a * √b(a≥0, b≥0)
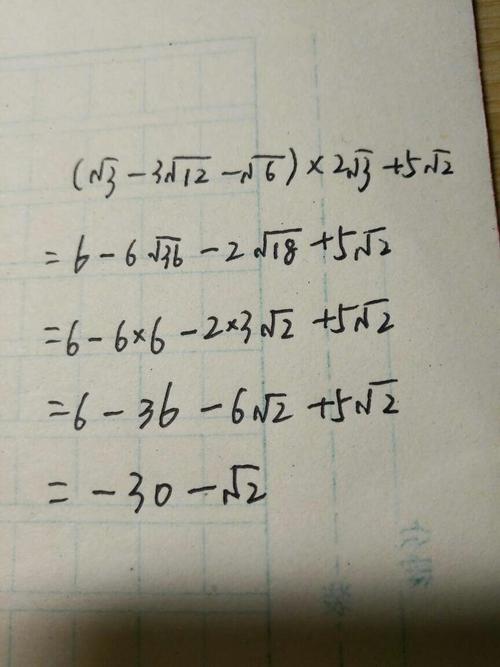
除法分配率:√(a÷b) = √a ÷ √b(b > 0)
根号的计算方法
1. 完全平方数的平方根
对于完全平方数,如4, 9, 16, ...,其平方根是整数,可以通过简单的算术运算得到。
2. 非完全平方数的平方根
对于非完全平方数,如2, 3, 5, ...,其平方根是无理数,通常使用计算器或数值逼近方法(如牛顿迭代法)来计算。
3. 立方根及更高次方根
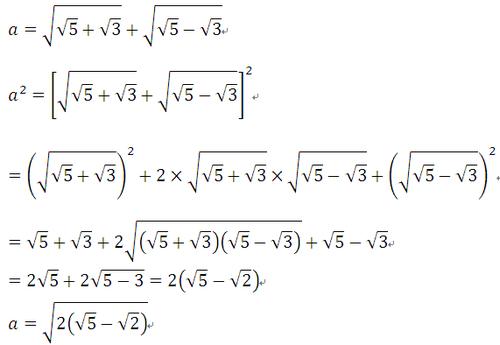
立方根及更高次方根的计算通常需要借助计算器或数学软件来完成,在数学分析中,有时会用到泰勒展开等高级方法来近似计算。
根号在生活中的应用实例
1. 物理学中的应用
运动学:在抛体运动的计算中,经常需要求解物体在特定时间或距离下的速度和加速度,这往往涉及到平方根的计算。
光学:光的折射率计算中,也会用到平方根来描述光在不同介质中传播速度的变化。
2. 工程技术中的应用
结构工程:在桥梁、建筑等结构的应力分析中,经常需要计算构件的受力情况,其中不乏平方根的运算。
电气工程:交流电的有效值(RMS)计算中,也使用了平方根的概念。
3. 经济金融中的应用
风险评估:在金融投资领域,标准差是衡量投资组合风险的重要指标之一,其计算过程中需要使用平方根。
资产定价:某些金融衍生品的定价模型中,如布莱克斯科尔斯期权定价公式,也包含了平方根的计算。
根号与其他数学概念的关联
1. 与指数的关系
平方根可以看作是指数的一种特殊形式,a的1/2次方等于√a,这种关系揭示了根号与指数之间的紧密联系。
2. 与方程的联系
在解代数方程时,经常会遇到需要求解变量的平方根或立方根的情况,这时,根号作为解题工具之一,发挥着关键作用。
3. 与函数的关系
平方根函数f(x) = √x是一个典型的示例函数,在微积分学中有着广泛的应用,研究它的导数、积分等性质有助于深入理解函数的本质特征。
根号作为数学中的基本运算符号之一,其重要性不言而喻,从定义到性质再到计算方法及其应用实例的介绍可以看出根号不仅具有深刻的理论意义还具有广泛的实用价值,无论是在科学研究还是在日常生活和技术应用中我们都能看到根号的身影感受到它带来的便利与魅力,因此掌握好根号的相关知识对于提高我们的数学素养和解决实际问题具有重要意义。
包含表格的说明
| 数值 | 平方根 (精确值或近似值) | 立方根 (精确值或近似值) |
| 4 | 2 | 1.587 |
| 9 | 3 | 2.080 |
| 16 | 4 | 2.520 |
| 2 | 1.414 | 1.260 |
| 8 | 2.828 | 2.000 |
| 27 | 5.196(精确值) | 3.000 |
注意:上表中对于非完全平方数和立方数的值进行了四舍五入处理以展示其近似值。
相关问题解答的FAQs
Q1: 如何计算负数的平方根?
A1: 在实数范围内,负数没有平方根,但在复数范围内,可以使用虚数单位i来表示负数的平方根。1的平方根是±i,这是因为i² = 1,±i)² = 1,对于其他负数a,其平方根可以表示为±√a * i,a是a的绝对值的平方根。
Q2: 为什么高次方根(如四次方根)在实数范围内总是有解?
A2: 高次方根(如四次方根)在实数范围内总是有解,是因为任何正实数的任何次方根(包括分数次方根和负次方根)都是定义良好的,并且可以通过幂的性质来理解和计算,对于四次方根√[4]a,它可以被理解为a^(1/4),这意味着找到一个数,当它自乘四次时等于a,根据实数的连续性和幂函数的性质,对于任何正实数a,都存在一个唯一的正实数b,使得b^4 = a,同样地,对于负实数也有对应的四次方根,但它们会落在复数域中。



