从基础到实用

想象一下：你正在规划家庭装修预算，需要平衡材料费、人工费和时间；或者你在分析市场数据，试图找出多个因素如何共同影响结果，这些看似不同的场景，背后都隐藏着一个共同的数学工具——线性方程组，掌握解法,就是掌握了一把打开现实问题之门的钥匙。

认识核心：何为线性方程组？

线性方程组是由多个包含相同变量的线性方程组合而成，一个“线性”方程意味着变量只以一次幂的形式出现（如 x, y），没有更复杂的乘积（如 xy）或高次幂（如 x²）,其标准形式通常写作：

a₁₁x₁ + a₁₂x₂ + ... + a₁ₙxₙ = b₁
a₂₁x₁ + a₂₂x₂ + ... + a₂ₙxₙ = b₂
...
aₘ₁x₁ + aₘ₂x₂ + ... + aₘₙxₙ = bₘ

• x₁, x₂, ..., xₙ 是我们需要求解的未知数。
• a₁₁, a₁₂, ..., aₘₙ 是已知的系数,表示每个未知数在方程中的权重。
• b₁, b₂, ..., bₘ 是已知的常数项。

解方程组的目标，就是找到一组具体的数值（x₁, x₂, ..., xₙ），使得代入方程组后，所有方程同时成立。

经典解法：手算的智慧

面对未知数较少的方程组（如2元或3元）,几种直观方法非常有效：

1. 代入消元法： 像侦探一样逐步追踪。

   • 从其中一个方程出发，将一个未知数用其他未知数表示，方程 2x + y = 8 中，解出 y = 8 - 2x。
   • 将这个表达式代入到另一个方程中，替换掉 y，代入方程 x - y = 1 得到 x - (8 - 2x) = 1。
   • 解这个只含 x 的新方程：x - 8 + 2x = 1 -> 3x = 9 -> x = 3。
   • 将求得的 x = 3 代回 y = 8 - 2x，得到 y = 8 - 6 = 2。
   • 解为 (x, y) = (3, 2)，最后务必代入原方程验证：2*3 + 2 = 8 成立，3 - 2 = 1 成立。

2. 加减消元法： 利用方程叠加简化。

   
   • 观察方程组，通过将方程乘以合适的数,使某个未知数的系数在两个方程中绝对值相等。
   • 将变换后的方程相加或相减,直接消去该未知数。

   • 方程1： 3x + 2y = 7
     方程2： 2x - y = 3

   • 将方程2乘以2：4x - 2y = 6。
   • 将方程1与新方程相加：(3x + 2y) + (4x - 2y) = 7 + 6 -> 7x = 13 -> x = 13/7。
   • 将 x = 13/7 代入方程2：2*(13/7) - y = 3 -> 26/7 - y = 21/7 -> -y = -5/7 -> y = 5/7。
   • 解为 (x, y) = (13/7, 5/7)。

3. 行列式法（克莱姆法则）： 适用于系数矩阵为方阵（方程数=未知数数）且行列式不为零的情况，公式直接给出每个未知数的解,对于二元方程组：

   a₁x + b₁y = c₁
   a₂x + b₂y = c₂

   解为： x = (c₁b₂ - c₂b₁) / (a₁b₂ - a₂b₁)y = (a₁c₂ - a₂c₁) / (a₁b₂ - a₂b₁) 分母就是系数矩阵的行列式，当方程规模增大时,计算量会显著增加。

强大工具：矩阵的力量

当未知数和方程数量增多（如工程计算、数据分析中的大规模问题），手算变得不切实际,矩阵和向量提供了简洁高效的表示和求解框架：

1. 矩阵表示： 将方程组写为 Ax = b。

   • A：系数矩阵（m x n 维）。
   • x：未知数向量（n x 1 维）。
   • b：常数项向量（m x 1 维）。

   • 2x + y - z = 1
     x - y + z = 2
     3x + 2y + z = 3

     可表示为： [ [2, 1, -1],[x][1][1, -1, 1],[y] = [2][3, 2, 1] ][z][3]

     

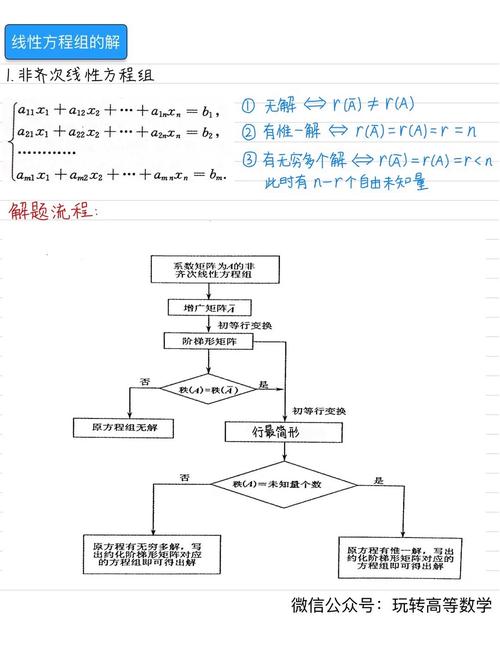
2. 高斯消元法： 这是计算机求解的基石,本质是系统化的加减消元。

   • 将增广矩阵 [A | b] 通过初等行变换（交换行、某行乘以非零常数、某行倍数加到另一行）化为行阶梯形。
   • 进一步化为简化行阶梯形（高斯-若尔当消元法）。
   • 从最后一行开始回代,依次求出所有未知数。
   • 此过程能清晰判断解的情况：唯一解、无穷多解（存在自由变量）、无解（出现矛盾方程如 0=1）。

3. 逆矩阵法： 当系数矩阵 A 是方阵且可逆（行列式不为零）时。

   • 解可表示为 x = A⁻¹b。
   • 先求出 A 的逆矩阵 A⁻¹，再与向量 b 相乘得到解向量 x。
   • 虽然概念清晰，但实际计算逆矩阵通常比高斯消元法效率低,尤其对于大型矩阵。

解的意义与应用场景

理解方程组解的情况至关重要：

• 唯一解： 所有方程约束条件精确地交汇于一点,根据成本和售价精确计算盈亏平衡点。
• 无穷多解： 方程描述的约束存在重叠或依赖，解形成一个空间（如直线、平面）,在资源分配中可能存在多种满足约束的组合。
• 无解： 方程描述的约束条件相互矛盾，没有同时满足的点,要求同时达到过高且相互冲突的性能指标。

线性方程组的力量渗透在众多领域：

• 工程计算： 结构力学中分析桥梁受力、电路分析中求解电流电压。
• 经济与金融： 投入产出模型分析产业链、投资组合优化平衡风险收益。
• 计算机科学： 计算机图形学的坐标变换、推荐算法中的协同过滤核心计算。
• 数据科学与机器学习： 线性回归模型拟合数据、求解优化问题的约束条件。
• 日常决策： 优化资源分配（如食材配比、时间规划）、平衡预算收支。

实用建议与工具选择

• 小规模问题： 优先考虑代入法或消元法,直观且计算量可控。
• 通用可靠方法： 高斯消元法及其变种（如选主元消元以提高数值稳定性）是解决中小规模问题的标准选择,也是理解解结构的基础。
• 大规模/数值计算： 依赖专业软件和库：
  • 编程语言库： Python（NumPy, SciPy 的 linalg.solve）、MATLAB、R 等提供高效且稳定的求解器。
  • 数学软件： Maple, Mathematica 提供强大的符号和数值计算能力。
  • 电子表格： Excel, Google Sheets 的矩阵函数 MINVERSE（求逆）和 MMULT（矩阵乘法）可求解较小规模问题（x = A⁻¹b）。
• 理解优于记忆： 掌握消元的思想（通过组合方程逐步简化）比死记公式更重要，理解解的存在性和唯一性条件（矩阵的秩）对于判断实际问题是否有解、解是否合理非常关键。

线性方程组并非停留在教科书中的抽象概念，而是连接数学理论与真实世界的实用桥梁，无论是工程师优化设计参数，还是普通人规划生活收支，理解其解法都能带来清晰的逻辑和更高的效率，面对复杂关系时，不妨尝试将其拆解为线性方程的形式，利用这些经典而强大的工具寻找答案，这种结构化分析问题的能力,往往比单纯获得计算结果更有价值。