如何排序
在计算机科学和数据处理中,排序是一种常见的操作,用于将一组数据按照某种特定顺序排列,根据不同的需求和数据特性,有多种排序算法可供选择,以下是几种常见的排序算法及其简要介绍:

1. 冒泡排序(Bubble Sort)
冒泡排序是一种简单的排序算法,它重复地遍历要排序的列表,比较每对相邻的元素,如果它们的顺序错误就交换位置,这个过程会持续到没有更多的元素需要交换,也就是说列表已经排序完成。
优点:
实现简单
对于小规模数据或基本有序的数据效率较高
缺点:
时间复杂度为O(n²),不适合大规模数据
不稳定排序
2. 选择排序(Selection Sort)
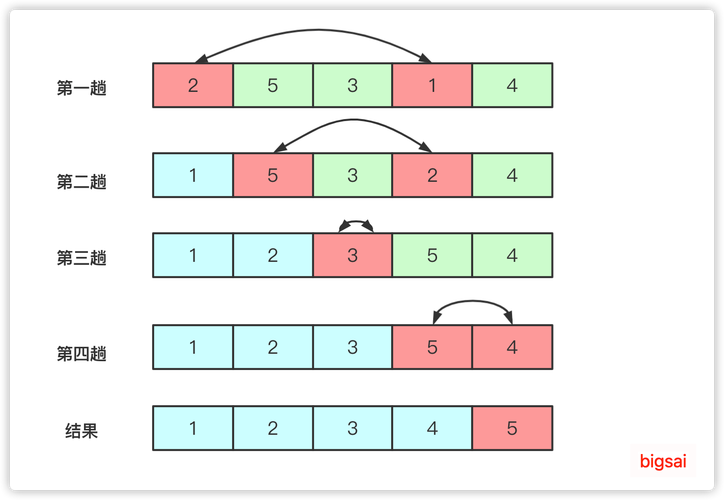
选择排序是一种简单直观的排序算法,它的工作原理是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
优点:
实现简单
对于小规模数据效率较高
缺点:
时间复杂度为O(n²)
不稳定排序
3. 插入排序(Insertion Sort)
插入排序是一种简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
优点:
实现简单
对于小规模数据或基本有序的数据效率较高
缺点:
时间复杂度为O(n²),不适合大规模数据
不稳定排序
4. 快速排序(Quick Sort)
快速排序是一种分治法(Divide and Conquer)策略来排序的算法,通过选择一个“基准”元素,将数组分为两部分,使得一部分的所有元素都比另一部分的元素小,然后递归地排序两个子部分。
优点:
平均时间复杂度为O(n log n)
适用于大规模数据集
原地排序(不需要额外的存储空间)
缺点:
最坏情况下时间复杂度为O(n²)
不稳定排序
5. 归并排序(Merge Sort)
归并排序也是一种采用分治策略的排序算法,它将问题分解成一些小问题,然后将小问题的解合并以创建大问题的解,归并排序将数组分成两半,对每一半进行递归排序,然后将结果合并在一起。
优点:
时间复杂度稳定为O(n log n)
稳定排序
缺点:
需要额外的存储空间
6. 堆排序(Heap Sort)
堆排序是一种基于二叉堆数据结构的比较排序算法,它首先将数组构造成一个最大堆,然后将堆顶的最大元素与末尾元素交换,并调整剩余元素为最大堆,重复此过程直到排序完成。
优点:
时间复杂度稳定为O(n log n)
原地排序(不需要额外的存储空间)
缺点:
不稳定排序
表格归纳
| 排序算法 | 时间复杂度(平均/最坏) | 空间复杂度 | 稳定性 | 适用场景 |
| 冒泡排序 | O(n²)/O(n²) | O(1) | 不稳定 | 小规模数据 |
| 选择排序 | O(n²)/O(n²) | O(1) | 不稳定 | 小规模数据 |
| 插入排序 | O(n²)/O(n²) | O(1) | 不稳定 | 小规模数据 |
| 快速排序 | O(n log n)/O(n²) | O(log n) | 不稳定 | 大规模数据 |
| 归并排序 | O(n log n)/O(n log n) | O(n) | 稳定 | 大规模数据 |
| 堆排序 | O(n log n)/O(n log n) | O(1) | 不稳定 | 大规模数据 |
相关问答FAQs
Q1: 如果数据已经接近排序状态,哪种排序算法更高效?
A1: 如果数据已经接近排序状态,插入排序通常更高效,因为插入排序在数据几乎已经排序的情况下,时间复杂度可以接近O(n),这使得它在处理这种情况时比其他O(n²)复杂度的算法更有效。
Q2: 当内存空间有限时,应该选择哪种排序算法?
A2: 当内存空间有限时,应该选择原地排序算法,如快速排序或堆排序,这些算法不需要额外的存储空间(除了少量的递归栈空间),而归并排序等非原地排序算法则需要额外的空间来合并已排序的子数组。