复利计算是金融领域中一个非常重要的概念,它涉及到资金的时间价值,复利是指投资者不仅可以获得本金的利息,还可以在之后的周期中获得之前累积利息的利息,这种“利滚利”的效应使得长期投资的收益非常可观,下面将详细介绍复利的计算方法、应用以及相关案例分析。
复利的基本概念
复利是指在一定时间内,不仅对初始投入的资金(本金)计算利息,而且对已经产生的利息也计算利息的一种计息方式,这与单利不同,单利只对本金计算利息,而不考虑已产生的利息。
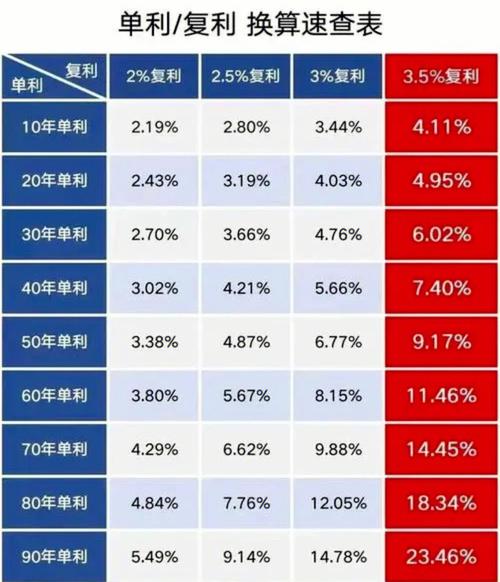
复利公式
复利的计算公式为:
\[ A = P (1 + \frac{r}{n})^{nt} \]
\( A \) 是未来值,即经过一段时间后的总金额。
\( P \) 是本金,即最初投入的资金。
\( r \) 是年利率。
\( n \) 是每年计息次数。
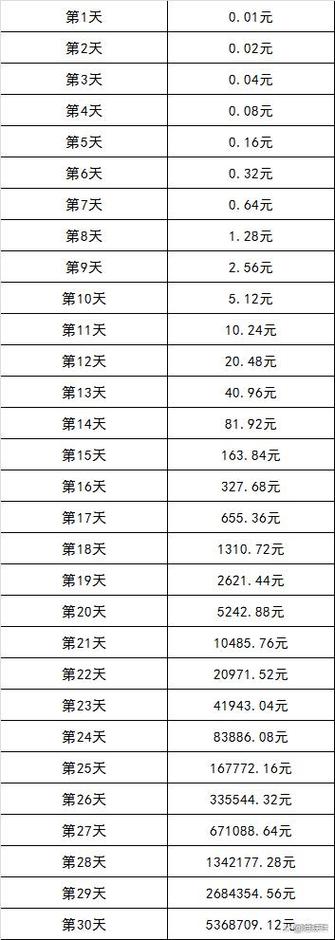
\( t \) 是时间,以年为单位。
复利的应用
3.1 储蓄账户
假设你在一个年利率为5%、每年计息一次的储蓄账户中存入1000元,那么5年后你的账户余额将是:
\[ A = 1000 \times (1 + 0.05)^5 = 1000 \times 1.27628 = 1276.28 \text{元} \]
3.2 投资回报
如果你投资了一笔钱,希望在10年后达到双倍的增长,可以使用复利公式来计算所需的年利率,设所需年利率为 \( r \),则有:
\[ 2P = P (1 + \frac{r}{n})^{10} \]
简化后得到:
\[ 2 = (1 + \frac{r}{n})^{10} \]
通过解这个方程可以得到所需的年利率。
复利的影响
复利的威力在于时间的积累,即使初始投资不大,只要持续投资并给予足够的时间,最终的收益也会非常显著,如果每月投资100元,年利率为6%,经过30年的复利增长,总金额将达到:
\[ A = 100 \times \left( \frac{(1 + \frac{0.06}{12})^{360} 1}{\frac{0.06}{12}} \right) \approx 72,409.25 \text{元} \]
复利计算表
| 年份 | 本金 | 利率 | 计息次数 | 总金额 |
| 0 | 1000 | 5% | 1 | 1000 |
| 1 | 1000 | 5% | 1 | 1050 |
| 2 | 1000 | 5% | 1 | 1102.5 |
| 3 | 1000 | 5% | 1 | 1157.6 |
| 4 | 1000 | 5% | 1 | 1215.5 |
| 5 | 1000 | 5% | 1 | 1276.3 |
FAQs
Q1: 什么是复利?
A1: 复利是一种计息方式,它不仅对本金计算利息,还对已经产生的利息计算利息,这意味着随着时间的推移,利息会不断累积并产生新的利息。
Q2: 如何利用复利进行投资?
A2: 要利用复利进行投资,首先需要选择一个合适的投资工具,如股票、债券或基金等,然后定期投入一定的资金,并保持长期持有,随着时间的推移,复利效应会使你的投资增值,重要的是要有耐心和坚持长期投资的理念。