长方形
公式:\(S = a \times b\)((a\)为长,\(b\)为宽)。
推导过程:将长方形沿着长边平均分成若干个小正方形,每个小正方形的边长为\(b\),一共有\(a\)个这样的小正方形,所以长方形的面积就是\(a\)个边长为\(b\)的小正方形的面积之和,即\(S = a \times b\)。
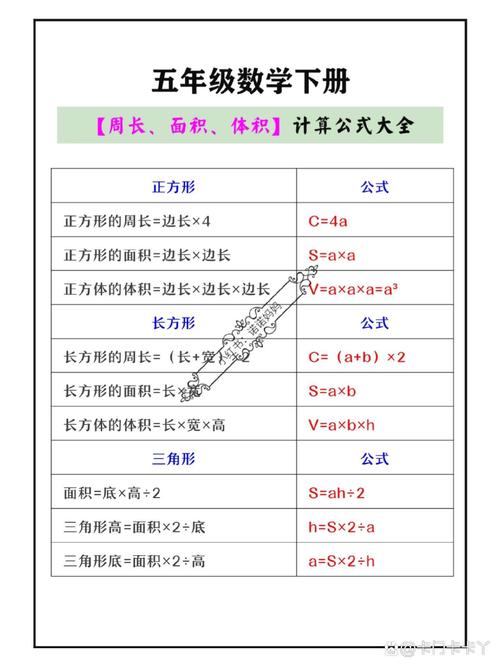
正方形
公式:\(S = a^2\)((a\)为边长)。
推导过程:正方形是特殊的长方形,四条边都相等,所以当长方形的长和宽都等于边长\(a\)时,就得到了正方形的面积公式\(S = a^2\)。
三角形
公式:\(S = \frac{1}{2}ah\)((a\)为底边长,\(h\)为底边上的高)。
推导过程:两个完全一样的三角形可以拼成一个平行四边形,平行四边形的底等于三角形的底,平行四边形的高等于三角形的高,因为平行四边形的面积等于底乘高,所以三角形的面积是等底等高的平行四边形面积的一半,即\(S = \frac{1}{2}ah\)。
平行四边形
公式:\(S = ah\)((a\)为底边长,\(h\)为底边上的高)。
推导过程:将平行四边形通过割补法转化为一个长方形,这个长方形的长等于平行四边形的底,长方形的宽等于平行四边形的高,因为长方形的面积等于长乘宽,所以平行四边形的面积等于底乘高,即\(S = ah\)。

梯形
公式:\(S = (a + b)h \div 2\)((a\)为上底,\(b\)为下底,\(h\)为高)。
推导过程:两个完全一样的梯形可以拼成一个平行四边形,这个平行四边形的底等于梯形的上底与下底之和,平行四边形的高等于梯形的高,因为平行四边形的面积等于底乘高,所以梯形的面积是拼成的平行四边形面积的一半,即\(S = (a + b)h \div 2\)。
圆形
公式:\(S = \pi r^2\)((r\)为半径,\(\pi\)取\(3.14\))。
推导过程:将圆平均分成若干个小扇形,当分的份数越多时,这些小扇形就越接近三角形,把这些小扇形拼成一个近似的长方形,长方形的长相当于圆周长的一半,即\(\pi r\),长方形的宽相当于圆的半径\(r\),因为长方形的面积等于长乘宽,所以圆的面积等于\(\pi r \times r = \pi r^2\)。
扇形
公式:\(S = \frac{n\pi r^2}{360}\)((n\)为圆心角的度数,\(r\)为半径)。
推导过程:扇形的面积是它所在圆的面积的一部分,圆心角为\(n^\circ\)的扇形面积是圆面积的\(\frac{n}{360}\),因为圆的面积是\(\pi r^2\),所以扇形的面积是\(S = \frac{n}{360} \times \pi r^2 = \frac{n\pi r^2}{360}\)。
椭圆
公式:\(S = \pi ab\)((a\)为长半轴长,\(b\)为短半轴长)。
推导过程:椭圆的面积公式可以通过积分等高等数学方法推导得出,但这里不进行详细推导,从直观上理解,椭圆可以看作是由两个半轴长度不同的椭圆形状构成,其面积与长短半轴的长度有关。
菱形
公式:\(S = \frac{d_1 d_2}{2}\)((d_1\)、\(d_2\)分别为对角线的长度)。
推导过程:菱形的对角线互相垂直平分,将菱形分成四个全等的直角三角形,每个直角三角形的两条直角边分别是两条对角线的一半,即\(\frac{d_1}{2}\)和\(\frac{d_2}{2}\),根据三角形的面积公式可得每个直角三角形的面积为\(\frac{1}{2} \times \frac{d_1}{2} \times \frac{d_2}{2} = \frac{d_1 d_2}{8}\),因为菱形由四个这样的直角三角形组成,所以菱形的面积是这四个直角三角形面积之和,即\(S = 4 \times \frac{d_1 d_2}{8} = \frac{d_1 d_2}{2}\)。
弓形
公式:当弧是劣弧时,\(S_{弓形} = S_{扇形} S_{\triangle AOB}\);当弧是半圆时,\(S_{弓形} = S_{扇形} = \frac{1}{2} \pi r^2\);当弧是优弧时,\(S_{弓形} = S_{扇形} + S_{\triangle AOB}\)。
推导过程:弓形是由一段弧和连接弧两端点的弦所围成的图形,当弧是劣弧时,弓形的面积等于扇形的面积减去由弦和两条半径所围成的三角形的面积;当弧是半圆时,弓形的面积就是半圆的面积;当弧是优弧时,弓形的面积等于扇形的面积加上由弦和两条半径所围成的三角形的面积。
为了帮助理解和应用上述面积计算公式,以下是两个常见问题及其解答:
1、如何计算一个复杂图形的面积?
答:可以将复杂图形分解成多个简单图形,分别计算这些简单图形的面积,然后将它们相加或相减,对于一个由长方形和三角形组成的图形,可以分别计算长方形和三角形的面积,然后将它们相加。
2、如何计算一个不规则图形的面积?
答:对于不规则图形,可以使用数值积分的方法来近似计算其面积,一种常用的方法是将图形分割成许多小矩形或三角形,然后求和这些小图形的面积,另一种方法是使用蒙特卡罗模拟等统计方法来估算面积。