分解质因数是一种将合数表示为若干个质数相乘的形式的方法,其中每个质数都是这个合数的因数,以下是关于如何分解质因数的详细解释:
一、定义与基本原理
定义:把一个合数分解成若干个质因数的乘积的形式,即求质因数的过程叫做分解质因数。

基本原理:每个合数都可以写成几个质数相乘的形式,其中每个质数都是这个合数的因数。
二、分解方法
短除法
短除法是分解质因数的一种常用方法,其步骤如下:
1、从最小的质数除起:首先用最小的质数(如2)去除待分解的合数,如果能整除,则记录下这个质数作为质因数,并用商继续进行下一步的分解;如果不能整除,则尝试下一个质数。
2、重复上述过程:重复上述步骤,直到商为质数为止。
3、特殊情况处理:如果待分解的合数是偶数,则首先用2去除,因为2是唯一的偶质数。

例子
以分解90为例,使用短除法的步骤如下:
| 被除数 | 除数 | 商 |
| 90 | 2 | 45 |
| 45 | 3 | 15 |
| 15 | 3 | 5 |
| 5 | 5 | 1 |
90=2×3×3×5。
三、其他算法与优化
除了短除法外,还有其他一些算法和优化方法可以用于分解质因数:
1、埃式筛法:通过筛选出小于等于√n的所有质数,然后利用这些质数来分解n。
2、线性筛法:在埃式筛法的基础上进行改进,进一步提高效率。
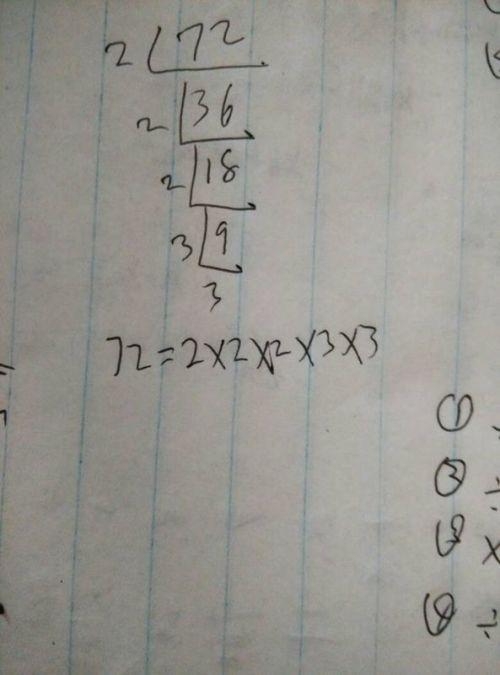
3、PollardRho算法:一种更高效的质因数分解算法,适用于大整数的分解。
四、注意事项
1、适用范围:分解质因数只针对合数,因为质数本身无法再分解为更小的质数。
2、唯一性:根据算术基本定理,任何一个大于1的自然数N如果N不为质数,那么N可以唯一分解成有限个质数的乘积。
五、实际应用
分解质因数在数学领域有广泛的应用,如求解最大公约数、最小公倍数等,它也是许多高级数学问题和算法的基础。
六、相关FAQs
Q1: 为什么分解质因数时要从最小的质数开始除起?
A1: 因为这样可以确保每次除尽后得到的商尽可能小且接近质数,从而加快分解过程并减少不必要的计算,从最小的质数开始也符合质因数分解的唯一性和有序性原则。
Q2: 如果一个合数的质因数中有多个相同的质因数,如何在分解结果中表示出来?
A2: 在分解结果中,相同质因数的个数可以通过指数的形式表示出来,如果一个合数可以分解为2×2×3×5,则可以简化表示为2^2×3×5,这种表示方式既简洁又清晰,能够准确反映合数的质因数构成情况。