为什么在使用Double时会出现报错？-HCRM博客

在计算机科学与编程领域，"double"类型的数据是常见的浮点数表示形式之一，它能够存储较大范围的数值，包括小数部分，在实际应用中，处理double类型数据时可能会遇到各种错误或问题，这些通常被称为“double报错”，本文将深入探讨double报错的类型、原因、解决方法以及如何避免它们，通过清晰的逻辑结构和丰富的信息量，为读者提供全面的指导。

一、double报错的类型与原因

（图片来源网络，侵权删除）

报错类型	描述	常见原因
溢出错误	计算结果超出double类型能表示的最大值或最小值。	运算涉及极大或极小数值，超过double范围。
下溢错误	计算结果接近于零，但不完全为零，导致精度问题。	运算结果太小，接近double类型的下限。
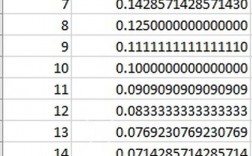
精度丢失	进行数学运算时，预期的小数精度未能保持。	浮点数表示限制，连续运算中的累积误差。
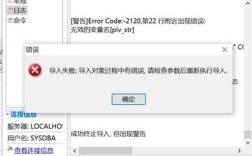
除以零错误	尝试除以零的操作。	分母为显式的0或因运算导致的数值极小，被视为0。
NaN（Not a Number）	运算结果不是一个合法的数字。	0除以0，或者负数的平方根等。
无穷大/无穷小	运算结果超出可表示的最大正值或最小负值。	如正数除以一个非常接近0的正数，可能得到正无穷。

二、解决策略与技巧

1、预防溢出与下溢：在进行计算前，检查操作数是否可能导致溢出或下溢，可以通过条件判断预先调整值或使用更高精度的数据类型（如BigDecimal）。

2、提高精度意识：理解并接受浮点数运算固有的精度限制，对于需要高精度的场合，考虑使用专门的数值库或数据类型。

3、避免直接比较浮点数：由于精度问题，直接比较两个浮点数是否相等往往不可靠，应采用epsilon（一个小的阈值）来比较两个浮点数之差是否足够小。

4、处理除以零：在执行除法操作前，确保分母不为零，或者在程序中加入异常处理机制。

5、识别并处理NaN与Infinity：利用编程语言提供的函数检查变量是否为NaN或Infinity，并根据业务逻辑做出相应处理。

（图片来源网络，侵权删除）

三、实践中的应用示例

以Python为例，展示如何处理一些常见的double报错情况：

import math
import numpy as np
检查是否为NaN
def is_nan(x):
    return math.isnan(x)
检查是否为无限大/小
def is_infinite(x):
    return math.isinf(x)
安全除法
def safe_divide(a, b):
    if b == 0:
        raise ValueError("Division by zero")
    return a / b
使用numpy进行向量化运算时的注意事项
arr = np.array([1e308, 1e308], dtype=np.float64)
print(np.sqrt(arr))  # 注意：即使输入是负数，numpy也会返回NaN而不是抛出错误

四、FAQs

Q1: 为什么浮点数运算会有精度问题？

A1: 浮点数在计算机内部是以二进制格式存储的，很多十进制下的小数在二进制转换时会变成无限循环小数，因此只能被近似表示，这种近似表示加上运算过程中的舍入误差，导致了精度问题。

Q2: 如何有效比较两个浮点数是否相等？