Nastran 报错问题在有限元分析中是常见且复杂的,需要系统化的方法和步骤来解决,以下将详细探讨 Nastran 报错的常见原因及解决方案:
常见 Nastran 报错及其原因
1、环境变量错误
错误描述:Nastran可执行文件不在由环境变量指定的位置。
解决方案:检查并设置正确的环境变量,确保 Nastran 可执行文件路径正确。
2、材料定义不完整
错误描述:材料定义不完整,例如缺少杨氏模量、剪切模量和泊松比。
解决方案:使用编辑材料命令添加缺失的材料属性。
3、欠约束模型
错误描述:由于枢轴比过大停止运行(错误9137)。
解决方案:添加“固定”约束或“沿曲面滑动”约束,避免横向移动和旋转。
4、迭代求解器问题
错误描述:无法使用迭代求解器进行处理。
解决方案:取消选中修改研究对话框中高级选项下的迭代求解器复选框。
5、几何体复杂性问题
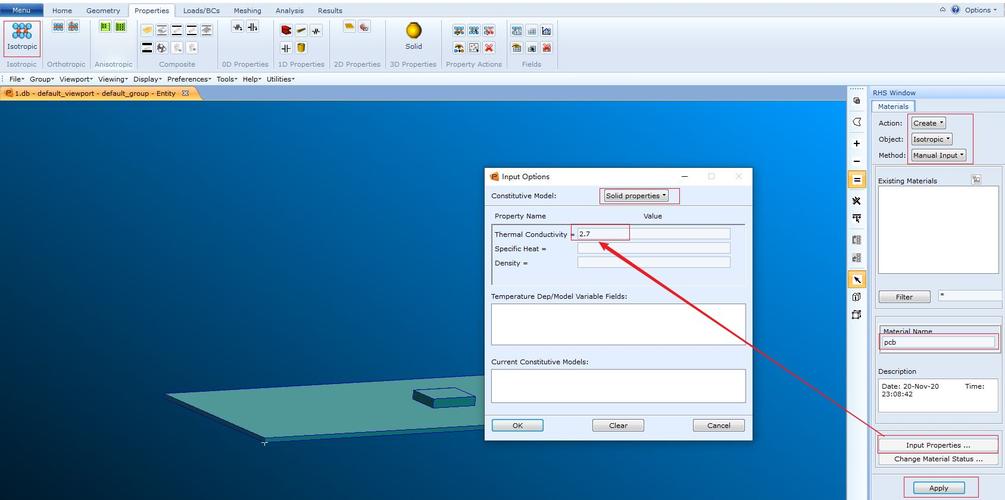
错误描述:由于网格大小和/或几何体复杂性问题,求解失败。
解决方案:优化网格,编辑研究处理参数,将“几何检查”选项设为“仅警告”。
6、连接件距离警告
错误描述:选定目标面和源面之间的距离超出指定距离。
解决方案:调整网格大小,使源侧上的网格比目标侧上的网格更小更密。
7、网格干涉
错误描述:封闭轴承和螺栓连接零件中的公称间隙。
解决方案:调整螺栓直径与孔径相等,移动零件使其物理对齐。
8、过度枢轴比
错误描述:RUN TERMINATED DUE TO EXCESSIVE PIVOT RATIOS IN MATRIX KLL。
解决方案:加对应的约束机制,或在 bdf 文件中添加 PARAM,BAILOUT,1 以继续运行。
具体错误案例及解决方法
1、NX Nastran NX2206.nastran 报错闪退
错误描述:报错信息为 invalid parameter passed to system or STL function。
可能原因:Nastran 可执行文件不在环境变量指定位置。
解决方案:检查并设置正确的环境变量,确保 Nastran 可执行文件路径正确。
2、PATRAN 2009 与 Nastran 报错 7340
错误描述:DMAP LTU logic even though datablock is still needed even though it is still needed。
可能原因:LTU 逻辑删除数据块导致的错误。
解决方案:尝试使用 SCR=yes 运行,或使用 DMAP 的 copy 在 alter 之前创建数据块副本。
3、Hypermesh 提交 Nastran 计算静强度模型错误 9050
错误描述:USER FATAL MESSAGE 9050(SEKRRS)。
可能原因:自由度约束不够,网格节点未连接。
解决方案:增加相应的约束,检查节点连接,或在 bdf 文件中添加 PARAM,BAILOUT,1。
常见问题解答 (FAQs)
1、为什么 Nastran 会因为环境变量错误而报错?
Nastran 依赖环境变量来定位其可执行文件,如果环境变量设置不正确,Nastran 将无法找到所需的程序文件,从而导致报错。
2、如何检查和设置 Nastran 的环境变量?
在操作系统的命令行中输入echo %PATH%(Windows)或echo $PATH(Linux/Unix),查看当前路径,确保 Nastran 可执行文件的路径包含在内,如果不在,可以通过修改.bashrc、.bash_profile 或系统设置来添加路径。
3、材料定义不完整会导致哪些具体错误?
材料定义不完整会导致静态分析、模态分析等计算无法进行,常见的错误包括材料属性缺失、材料类型不匹配等。
4、如何解决 Nastran 的欠约束模型问题?
欠约束模型通常表现为某些自由度过多,导致解算过程中出现奇异矩阵,通过添加适当的约束(如固定约束、沿曲面滑动约束等)可以解决此类问题。
5、如何优化几何体复杂性导致的 Nastran 报错?
几何体复杂性问题通常与网格划分有关,可以通过优化网格划分策略,如调整网格大小、简化几何体等方式来解决,还可以在求解设置中将“几何检查”选项设为“仅警告”,以允许一定程度的几何复杂性。
Nastran 报错问题涉及多个方面,包括环境变量设置、材料定义完整性、模型约束、几何体复杂性等,通过系统化的排查方法和针对性的解决方案,可以有效解决这些问题,提高有限元分析的准确性和可靠性。











