一、立方的概念
立方是指一个数或图形在三维空间中的三次方,在数学中,一个数的立方是将该数自乘三次的结果;在几何学中,立方体的体积就是其边长的立方。
二、立方的计算公式
1、对于立方体:体积等于边长的立方,公式为\(V = a^3\),(V\)表示体积,\(a\)表示立方体的边长。
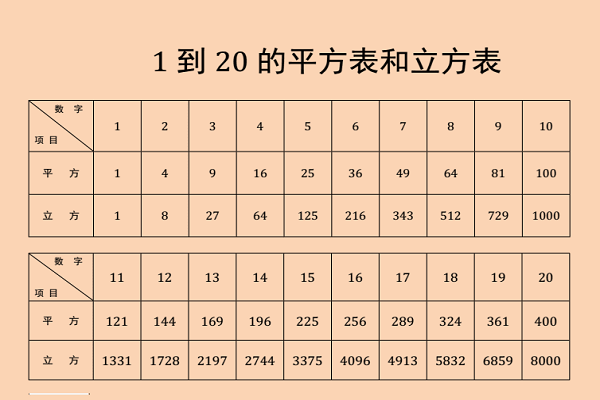
2、对于一个数:它的立方可以表示为\(a^3\),即该数乘以自身两次。
三、常见的立方计算方法
1、直接计算法:选择一个数\(n\),先将其与自身相乘得到\(n^2\),再将\(n^2\)与\(n\)相乘,即可得到立方数\(n^3\)。
2、公式法:利用公式\(n^3 = n × n × n\)进行计算,适用于大数的计算。
3、使用计算器:现代计算器通常都有计算立方的功能,可直接输入数值得到结果。
4、查找立方表:在一些数学工具书中,会有立方数的表格,可查找对应数的立方值。
四、不同类型数字的立方计算示例
1、整数:如计算5的立方,\(5×5 = 25\),\(25×5 = 125\),(5^3 = 125\)。
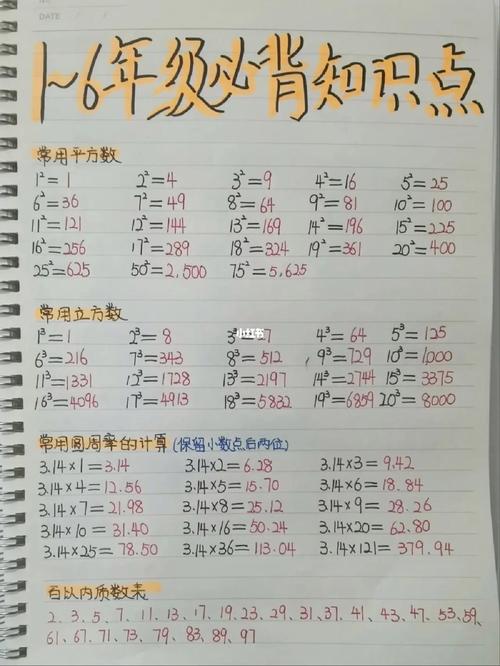
2、小数:如计算0.2的立方,\(0.2×0.2 = 0.04\),\(0.04×0.2 = 0.008\),则\(0.2^3 = 0.008\)。
3、分数:如计算\((\frac{1}{2})^3\),先计算分子的立方\(1^3 = 1\),再除以分母的立方\(2^3 = 8\),结果为\((\frac{1}{2})^3 = \frac{1}{8}\)。
4、负数:如计算\((3)^3\),\((3)×(3) = 9\),\(9×(3) = 27\),((3)^3 = 27\)。
五、立方在实际中的应用
1、几何学:用于计算立方体的体积,从而确定物体所占空间的大小。
2、物理学:在某些物理问题中,如计算物体的转动惯量等,可能会用到立方计算。
3、工程学:在设计和建造一些具有立方体形状的结构时,需要计算其体积和表面积等参数。

4、统计学:可用于描述数据的分布情况,例如计算所有数据的立方数可以得到方差,方差是衡量数据变异程度的指标。
5、计算机科学:常用于算法分析和数据结构设计,对数据进行立方操作可实现特定的逻辑和功能。
六、相关问题解答
1、什么是立方根?立方根与立方有什么关系?
答:如果一个数的立方等于\(a\),那么这个数就叫做\(a\)的立方根,用数学符号表示为\(\sqrt[3]{a}\),立方根与立方互为逆运算,即如果\(x^3 = a\),(x = \sqrt[3]{a}\)。
2、如何快速判断一个数是否是完全立方数?
答:可以通过观察该数的因数分解来判断,如果一个数的所有质因数都是三个一组重复出现的,那么这个数就是完全立方数,\(64 = 2^6 = (2^2)^3 = 4^3\),所以64是完全立方数。